Contour stencils weighted L1 demosaicing. More...

#include <math.h>
#include <string.h>
#include "basic.h"
#include "conv.h"
#include "inv3x3.h"
#include "dmbilinear.h"
#include "mstencils.h"
#include "dmcswl1.h"

Include dependency graph for dmcswl1.c:

Go to the source code of this file.

Macros
#define	GAMMA1 4
	Penalty term weight to enforce 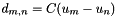$d_{m,n} = C(u_m - u_n)$ . More...

#define	GAMMA2 256
	Penalty term weight to enforce observation constraint. More...

#define	NUMNEIGH 8
	How many adjacent neighbors a node has. More...

#define	NUMORIENTATIONS 8
	How many distinct orientations are detected. More...

#define	MU (GAMMA2/(2NUMNEIGHGAMMA1))
	mu = gamma_2 / (2 NUMNEIGH gamma_1) More...

Functions
void	DShrink (float(d)[NUMNEIGH][3], float(dtilde)[NUMNEIGH][3], const float Image, float(Weight)[NUMNEIGH], int Width, int Height, float Alpha)
	Solves the d-subproblem. More...

float	UGaussSeidel (float Image, float b, float(dtilde)[NUMNEIGH][3], const float Mosaic, int Width, int Height, int RedX, int RedY)
	Solves the u-subproblem. More...

int	ConstructGraph (float(Weight)[NUMNEIGH], const float Mosaic, int Width, int Height, int RedX, int RedY, float Epsilon, float Sigma)
	Construct the weighted graph according to contour orientations. More...

void	CopyCfaValues (float Image, const float Mosaic, int Width, int Height, int RedX, int RedY)
	Copy image components that are known from the input mosaiced data. More...

float	EvaluateCSWL1Energy (const float Image, int Width, int Height, int RedX, int RedY, float Alpha, float(Weight)[NUMNEIGH], const float *Mosaic)
	Evaluate the contour stencils demosaicking energy function. More...

int	CSWL1Demosaic (float *Image, int Width, int Height, int RedX, int RedY, float Alpha, float Epsilon, float Sigma, float Tol, int MaxIter, int ShowEnergy)
	Contour stencils weighted L1 demosaicing. More...

Detailed Description

Contour stencils weighted L1 demosaicing.

Author: Pascal Getreuer getre.nosp@m.uer@.nosp@m.gmail.nosp@m..com

This file implements the image demosaicing method as described in IPOL article "Image Demosaicking with Contour Stencils." The main computation is in routine CSWL1Demosaic.

This program is free software: you can use, modify and/or redistribute it under the terms of the simplified BSD License. You should have received a copy of this license along this program. If not, see http://www.opensource.org/licenses/bsd-license.html.

Definition in file dmcswl1.c.

Macro Definition Documentation

#define GAMMA1 4

Penalty term weight to enforce $d_{m,n} = C(u_m - u_n)$ .

Definition at line 31 of file dmcswl1.c.

#define GAMMA2 256

Penalty term weight to enforce observation constraint.

Definition at line 33 of file dmcswl1.c.

#define MU (GAMMA2/(2*NUMNEIGH*GAMMA1))

mu = gamma_2 / (2 NUMNEIGH gamma_1)

Definition at line 46 of file dmcswl1.c.

#define NUMNEIGH 8

How many adjacent neighbors a node has.

Note: Changing this constant requires revision of the code

Definition at line 38 of file dmcswl1.c.

#define NUMORIENTATIONS 8

How many distinct orientations are detected.

Note: Changing this constant requires revision of the code

Definition at line 43 of file dmcswl1.c.

Function Documentation

int ConstructGraph	(	float(*)	Weight[NUMNEIGH],
		const float *	Mosaic,
		int	Width,
		int	Height,
		int	RedX,
		int	RedY,
		float	Epsilon,
		float	Sigma
	)

Construct the weighted graph according to contour orientations.

Parameters

Weight	the edge weights of the graph
Mosaic	the input mosaiced image
Width,Height	the image dimensions
RedX,RedY	the coordinates of the upper-leftmost red pixel
Epsilon	edge weight for weak links in the graph
Sigma	graph filtering parameter

This function constructs the weighted graph that will be used for the graph regularization in the contour stencil demosaicking.

Each interior pixel has eight neighbors. The neighborhood is enumerated in counter-clockwise order beginning with the right adjacent neighbor.

 3      2      1
   `.   |   .`
     `. | .`
 4 -----+----- 0
     .` | `.
   .`   |   `.
 5      6      7

The graph edge weights over this neighborhood for different local contour orientations are stored in NeighWeights.

Definition at line 545 of file dmcswl1.c.

Here is the call graph for this function:

Here is the caller graph for this function:

void CopyCfaValues	(	float *	Image,
		const float *	Mosaic,
		int	Width,
		int	Height,
		int	RedX,
		int	RedY
	)

Copy image components that are known from the input mosaiced data.

Parameters

Image	the input RGB image in planar row-major order
Mosaic	the input mosaiced image
Width,Height	the image dimensions
RedX,RedY	the coordinates of the upper-leftmost red pixel

This function is used to set the components of Image equal to the values that are known from the input mosaiced image,

$u_m^k = f_m, m \in \Omega^k, k \in \{R,G,B\}.$

Definition at line 624 of file dmcswl1.c.

Here is the caller graph for this function:

int CSWL1Demosaic	(	float *	Image,
		int	Width,
		int	Height,
		int	RedX,
		int	RedY,
		float	Alpha,
		float	Epsilon,
		float	Sigma,
		float	Tol,
		int	MaxIter,
		int	ShowEnergy
	)

Contour stencils weighted L1 demosaicing.

Parameters

Image	the input RGB image in planar row-major order
Width,Height	the image dimensions
RedX,RedY	the coordinates of the upper-leftmost red pixel
Alpha	weight on the chromatic term
Epsilon	edge weight for weak links in the graph
Sigma	graph filtering parameter
Tol	stopping tolerance
MaxIter	maximum number of iterations
ShowEnergy	if nonzero, display the energy value after each iteration

Returns: 1 on success, 0 on failure

This is the main computation routine for contour stencils demosaicing. It solves the minimization

$\left\{ \begin{aligned} \operatorname*{arg\,min}_{d,u} & \sum_m \Bigl(\sum_n \bigl(w_{m,n} d^L_{m,n} \bigr)^2\Bigr)^{1/2} + \alpha \sum_m \Bigl(\sum_n \Bigl(w_{m,n} \sqrt{(d^{C1}_{m,n})^2 + (d^{C2}_{m,n})^2} \,\Bigr)^2\Bigr)^{1/2} \\ \text{subject to} \; & d_{m,n} = C(u_m - u_n), \; m,n\in\mathbb{Z}^2, \\ & u_m^{k} = f_m, \; m\in\Omega^k, k\in\{R,G,B\}, \end{aligned}\right.$

by Bregman iteration. This is done by alternatingly solving the D-subproblem with DShrink and the U-subproblem with UGaussSeidel.

Definition at line 750 of file dmcswl1.c.

Here is the call graph for this function:

Here is the caller graph for this function:

void DShrink	(	float(*)	d[NUMNEIGH][3],
		float(*)	dtilde[NUMNEIGH][3],
		const float *	Image,
		float(*)	Weight[NUMNEIGH],
		int	Width,
		int	Height,
		float	Alpha
	)

Solves the d-subproblem.

Parameters

d	the previous solution of d, updated by this routine
dtilde	the previous dtilde, updated by this routine
Image	the current solution of the demosaiced image
Weight	the edge weights of the graph
Width,Height	the image dimensions
Alpha	weight on the chromatic term

The d variable subproblem is

$\begin{aligned} \operatorname*{arg\,min}_{d} & \sum_m \Bigl(\sum_n \bigl(w_{m,n} d^L_{m,n} \bigr)^2\Bigr)^{1/2} + \alpha \sum_m \Bigl(\sum_n \Bigl(w_{m,n} \sqrt{(d^{C1}_{m,n})^2 + (d^{C2}_{m,n})^2} \,\Bigr)^2\Bigr)^{1/2} \\ & {+}\,\, \frac{\gamma_1}{2} \sum_{m,n} \|\tilde{d}_{m,n} - C(u_m - u_n)\|_2^2 \end{aligned}$

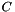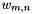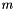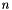where $ C $ is the color transform matrix, and $w_{m,n}$ denote the graph weights between pixels $ m $ and $ n $ . The problem decouples over m and also decouples between the luminosity channel L and the chromatic channels C1 and C2. This leads to subproblems of the form

$\operatorname*{arg\,min}_{x\in\mathbb{R}^N} \, \Bigl( \sum_{n=1}^N (w_n x_n)^2 \Bigr)^{1/2} + \frac{\gamma}{2} \sum_{n=1}^N (x_n - y_n)^2.$

The minimizer of this problem satisfies

$w_m^2 x_m = \gamma (y_m - x_m) \lVert x \rVert_w, \quad \lVert x \rVert_w := \Bigl( \sum_{n=1}^N (w_n x_n)^2 \Bigr)^{1/2}.$

We can approximate the solution by fixed point iteration,

$x_m^\text{next} = y_m \frac{\gamma \lVert x \rVert_w} {w_m^2 + \gamma \lVert x \rVert_w},$

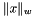where $\|x\|_w$ is computed using on the solution from the previous Bregman iteration or, if it is the first iteration or the previous solution was 0, as $\|y\|_w$ .

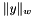The update of 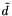$\tilde{d}$ is computed as

$\tilde{d}_{m,n}^\text{next} = \tilde{d}_{m,n} - C(u_m - u_n) + 2d_{m,n}^\text{next} - d_{m,n}.$

Definition at line 259 of file dmcswl1.c.

Here is the caller graph for this function:

float EvaluateCSWL1Energy	(	const float *	Image,
		int	Width,
		int	Height,
		int	RedX,
		int	RedY,
		float	Alpha,
		float(*)	Weight[NUMNEIGH],
		const float *	Mosaic
	)

Evaluate the contour stencils demosaicking energy function.

Parameters

Image	the input RGB image in planar row-major order
Width,Height	the image dimensions
RedX,RedY	the coordinates of the upper-leftmost red pixel
Alpha	weight on the chromatic term
Weight	the edge weights of the graph
Mosaic	the input mosaiced image

Returns: Energy value

This routine evaluates the energy function to be minimized by the contour stencil weighted-L1 demosaicking,

$E(u) = \sum_m \Bigl(\sum_n \bigl(w_{m,n} \lVert u_m - u_n \rVert_L \bigr)^2\Bigr)^{1/2} + \alpha \sum_m \Bigl(\sum_n \bigl(w_{m,n} \lVert u_m - u_n \rVert_C \bigr)^2\Bigr)^{1/2},$

where in this computation, u is forced to agree with the mosaiced input data on the CFA, 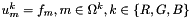$u_m^k = f_m, m \in \Omega^k, k \in \{R,G,B\}$ .

When the CSWL1Demosaic() is called with ShowEnergy set to a nonzero value, the energy value is displayed after each Bregman iteration. This can be used to check the convergence of the minimization.

Definition at line 670 of file dmcswl1.c.

Here is the call graph for this function:

Here is the caller graph for this function:

float UGaussSeidel	(	float *	Image,
		float *	b,
		float(*)	dtilde[NUMNEIGH][3],
		const float *	Mosaic,
		int	Width,
		int	Height,
		int	RedX,
		int	RedY
	)

Solves the u-subproblem.

Parameters

Image	the demosaiced image solution (u), updated by this routine
b	the Bregman auxiliary variable, updated by this routine
dtilde	current dtilde
Mosaic	the input mosaiced image
Width,Height	the image dimensions
RedX,RedY	the coordinates of the upper-leftmost red pixel

Returns: L^2 difference between the previous Image and updated Image

The current demosaicking solution, Image (u), is updated by approximately solving the u subproblem using Gauss-Seidel. The solution satisfies

$\begin{aligned} & (2\cdot 8\gamma_1 C^*C + \gamma_2 e_m e_m^T) u_m^\text{next} = \\ & \quad \gamma_1 \sum_n C^*(2C u_n + \tilde{d}_{m,n} - \tilde{d}_{n,m}) + \gamma_2 e_m (f_m - b_m), \end{aligned}$

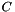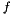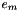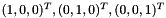where $ C $ is the color transform matrix, $ f $ is the input mosaiced image (Mosaic), and $ e_m $ is $ (1,0,0)^T, (0,1,0)^T, (0,0,1)^T $ respectively at red, green, and blue locations. Inverses of the matrices

$(2\cdot 8\gamma_1 C^*C + \gamma_2 e_m e_m^T)$

are precomputed.

Definition at line 384 of file dmcswl1.c.

Here is the caller graph for this function:

Macros

Functions

Detailed Description

Macro Definition Documentation

Function Documentation