|
Image Interpolation with Geometric Contour Stencils
|
|
Image Interpolation with Geometric Contour Stencils
|
Compute the singular value decomposition of a 2x2 matrix. More...

Go to the source code of this file.
Functions | |
| void | Svd2x2 (double *Theta, double *Sigma1, double *Sigma2, double *Phi, int *Sign1, int *Sign2, double A[2][2]) |
| Compute the singular value decomposition of a 2x2 matrix. More... | |
Compute the singular value decomposition of a 2x2 matrix.
Copyright (c) 2010-2011, Pascal Getreuer All rights reserved.
This program is free software: you can use, modify and/or redistribute it under the terms of the simplified BSD License. You should have received a copy of this license along this program. If not, see http://www.opensource.org/licenses/bsd-license.html.
Definition in file svd2x2.h.
| void Svd2x2 | ( | double * | Theta, |
| double * | Sigma1, | ||
| double * | Sigma2, | ||
| double * | Phi, | ||
| int * | Sign1, | ||
| int * | Sign2, | ||
| double | A[2][2] | ||
| ) |
Compute the singular value decomposition of a 2x2 matrix.
| Theta | rotation of the U matrix |
| Sigma1,Sigma2 | singular values |
| Phi | rotation of the V matrix |
| Sign1,Sign2 | correction signs |
| A | input 2x2 matrix |
Computes the singular value decomposition of A,
![\[ A = U \Sigma V^T. \]](form_45.png)
U is a rotation by Theta,
![\[ U = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}. \]](form_46.png)
Sigma is the diagonal matrix with entries Sigma1 and Sigma2, which satisfy Sigma1 >= Sigma2 >= 0. V is in general not representable by a rotation alone and is further decomposed as a rotation matrix W and a diagonal sign correction matrix C so that
![\[ A = U \Sigma C W^T. \]](form_47.png)
W is a rotation by Phi,
![\[ W = \begin{pmatrix} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{pmatrix}, \]](form_48.png)
and C is
![\[ C = \begin{pmatrix} \text{Sign1} & 0 \\ 0 & \text{Sign2} \end{pmatrix}, \]](form_49.png)
where Sign1 and Sign2 are signs, values of either +1 or -1.
The matrices U and V can be computed from Theta, Phi, Sign1, Sign2 as
The algorithm used here is based on the notes http://www.ualberta.ca/~mlipsett/ENGM541/Readings/svd_ellis.pdf. The derivation is, first, by expanding the following in terms of the components
![\[ \begin{pmatrix} a & b \\ b & c \end{pmatrix} = A A^T = U \Sigma^2 U^T, \]](form_50.png)
one can show
![\[ \begin{aligned} 2b &= (\sin 2\theta)(\sigma_1^2 - \sigma_2^2), \\ a - c &= (\cos 2\theta)(\sigma_1^2 - \sigma_2^2). \end{aligned} \]](form_51.png)
Therefore,
![\[ \theta = \tfrac{1}{2} \mathrm{atan2}(2b, a - c), \]](form_52.png)
and similarly for 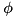 with
with 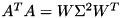 .
.
Second, now that U and W are known, the singular values and signs are obtained as
![\[ \Sigma C = U^T A W \]](form_55.png)
 1.8.3.1
1.8.3.1