u-subproblem DCT solver for TV-regularized deconvolution More...

#include <string.h>
#include "util_deconv.h"

Functions
static void	AdjBlurDct (num ATrans, FFT(plan) TransformA, const num KernelTrans, int Width, int Height, int NumChannels, num Alpha)
	Compute 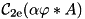$\mathcal{C}_\mathrm{2e}(\alpha \varphi * A)$ . More...

static int	InitDeconvDct (tvregsolver *S)
	Intializations to prepare TvRestore for DCT-based deconvolution. More...

static void	UTransSolveDct (num BTrans, num B, FFT(plan) TransformB, num ATrans, const numvec2 dtilde, const num *DenomTrans, int Width, int Height, int NumChannels)
	Compute BTrans = ( ATrans - DCT[div(dtilde)] ) / DenomTrans. More...

static num	UDeconvDct (tvregsolver *S)
	Solve the u subproblem using DCT transforms (UseZ = 0) More...

static num	UDeconvDctZ (tvregsolver *S)
	Solve the u subproblem using DCT transforms (UseZ = 1) More...

Detailed Description

u-subproblem DCT solver for TV-regularized deconvolution

Author: Pascal Getreuer getre.nosp@m.uer@.nosp@m.gmail.nosp@m..com

This program is free software: you can use, modify and/or redistribute it under the terms of the simplified BSD License. You should have received a copy of this license along this program. If not, see http://www.opensource.org/licenses/bsd-license.html.

Definition in file usolve_dct_inc.c.

Function Documentation

static void AdjBlurDct	(	num *	ATrans,
		FFT(plan)	TransformA,
		const num *	KernelTrans,
		int	Width,
		int	Height,
		int	NumChannels,
		num	Alpha
	)

static

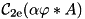Compute $\mathcal{C}_\mathrm{2e}(\alpha \varphi * A)$ .

Parameters

ATrans	the destination
TransformA	FFTW plan, transforming A to ATrans
KernelTrans	the transform of the convolution kernel
Width,Height,NumChannels	image dimensions
Alpha	positive scalar

As an intermediate computation for the u subproblem, this routine computes 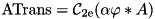$\mathrm{ATrans}= \mathcal{C}_\mathrm{2e}(\alpha \varphi * A)$ .

Definition at line 29 of file usolve_dct_inc.c.

static int InitDeconvDct ( tvregsolver * S )

static

Intializations to prepare TvRestore for DCT-based deconvolution.

Parameters

S	tvreg solver state

Returns: 1 on success, 0 on failure

This routine sets up FFTW transform plans and precomputes the transform 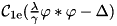$\mathcal{C}_\mathrm{1e}(\frac{\lambda}{\gamma}\varphi * \varphi-\Delta)$ in S->DenomTrans. If UseZ = 0, the transform 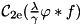$\mathcal{C}_\mathrm{2e}(\frac{\lambda}{\gamma}\varphi *f)$ is precomputed in S->ATrans.

Definition at line 58 of file usolve_dct_inc.c.

static num UDeconvDct ( tvregsolver * S )

static

Solve the u subproblem using DCT transforms (UseZ = 0)

Parameters

S	tvreg solver state

This routine solves the u-subproblem

$\tfrac{\lambda}{\gamma}\varphi *\varphi *u -\Delta u = \tfrac{\lambda}{ \gamma}\varphi *f -\operatorname{div}\tilde{d}.$

The solution is obtained using discrete cosine transforms (DCTs) as

$u=\mathcal{C}_\mathrm{2e}^{-1}\left[\frac{\mathcal{C}_\mathrm{2e} \bigl(\frac{\lambda}{\gamma}\varphi *f-\operatorname{div}\tilde{d}\bigr)}{ \mathcal{C}_\mathrm{1e}(\frac{\lambda}{\gamma}\varphi *\varphi-\Delta)} \right],$

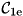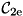where $\mathcal{C}_\mathrm{1e}$ and $\mathcal{C}_\mathrm{2e}$ denote the DCT-I and DCT-II transforms of the same period lengths. Two of the above quantities are precomputed by InitDeconvDct(): the transform of 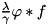$\frac{\lambda}{\gamma}\varphi *f$ is stored in S->ATrans and the transformed denominator is stored in S->DenomTrans.

Definition at line 196 of file usolve_dct_inc.c.

static num UDeconvDctZ ( tvregsolver * S )

static

Solve the u subproblem using DCT transforms (UseZ = 1)

Parameters

S	tvreg solver state

This extended version of UDeconvDct() is used when performing DCT-based deconvolution with the three-auxiliary variable algorithm (UseZ = 1). The u subproblem in this case is

$\tfrac{\gamma_2}{\gamma_1}\varphi *\varphi *u -\Delta u = \tfrac{ \gamma_2}{\gamma_1}\varphi *\tilde{z} -\operatorname{div}\tilde{d}.$

Compared to UDeconvDct(), the main differences are that the DCT of ztilde is computed and 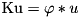$\mathrm{Ku} = \varphi * u$ is updated.

Definition at line 221 of file usolve_dct_inc.c.

static void UTransSolveDct	(	num *	BTrans,
		num *	B,
		FFT(plan)	TransformB,
		num *	ATrans,
		const numvec2 *	dtilde,
		const num *	DenomTrans,
		int	Width,
		int	Height,
		int	NumChannels
	)

static

Compute BTrans = ( ATrans - DCT[div(dtilde)] ) / DenomTrans.

This subroutine is a part of the DCT u-subproblem solution that is common to both the d,u splitting (UseZ = 0) and d,u,z splitting (UseZ = 1).

Definition at line 157 of file usolve_dct_inc.c.

Functions

Detailed Description

Function Documentation