z-subproblem solvers for restoration with non-Gaussian noise models More...

Functions
static void	ZSolveL1 (tvregsolver *S)
	Solve the z-subproblem with a Laplace (L1) noise model. More...

static void	ZSolveL2 (tvregsolver *S)
	Solve the z-subproblem with a Gaussian (L2) noise model. More...

static void	ZSolvePoisson (tvregsolver *S)
	Solve the z-subproblem with a Poisson noise model. More...

Detailed Description

z-subproblem solvers for restoration with non-Gaussian noise models

Author: Pascal Getreuer getre.nosp@m.uer@.nosp@m.gmail.nosp@m..com

This file has routines for solving the z subproblem. These routines are used only when either

the noise model is non-Gaussian,

the restoration problem has both deconvolution and spatially-varying lambda (e.g., simultaneous deconvolution-inpainting).

Otherwise, the restoration problem is solved with a simpler d,u splitting. The variable tvregsolver::UseZ indicates whether the restoration includes a z subproblem.

The general form of the z subproblem is

$\operatorname*{arg\,min}_{z}\,\lambda\sum_{i,j}F(z_{i,j},f_{i,j}) +\frac{\gamma_2}{2}\sum_{i,j}(z_{i,j}-u_{i,j}-b^2_{i,j})^2,$

where F depends on the noise model and the second term is a penalty to encourage the constraint z = u. The optimal z is the solution of

$\lambda\partial_z F(z,f) + \gamma_2(z - u - b^2) = 0.$

This program is free software: you can use, modify and/or redistribute it under the terms of the simplified BSD License. You should have received a copy of this license along this program. If not, see http://www.opensource.org/licenses/bsd-license.html.

Definition in file zsolve_inc.c.

Function Documentation

static void ZSolveL1 ( tvregsolver * S )

static

Solve the z-subproblem with a Laplace (L1) noise model.

Parameters

S	tvregsolver state

This routine solves the z-subproblem with Laplace noise model to update z,

$\operatorname*{arg\,min}_{z}\,\lambda\sum_{i,j}\lvert z_{i,j}-f_{i,j} \rvert+\frac{\gamma_2}{2}\sum_{i,j}(z_{i,j}-u_{i,j}-b^2_{i,j})^2.$

The auxiliary variable 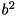$ b^2 $ is also updated according to

$b^2 = b^2 + u - z.$

Instead of representing 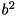$ b^2 $ directly, we use 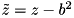$\tilde{z}=z-b^2$ , which is algebraically equivalent but requires less arithmetic.

static void ZSolveL2 ( tvregsolver * S )

static

Solve the z-subproblem with a Gaussian (L2) noise model.

Parameters

S	tvregsolver state

Solves the z-subproblem with Gaussian noise model to update z,

$\operatorname*{arg\,min}_{z}\,\frac{\lambda}{2}\sum_{i,j}(z_{i,j}- f_{i,j})^2+\frac{\gamma_2}{2}\sum_{i,j}(z_{i,j}-u_{i,j}-b^2_{i,j})^2.$

The auxiliary variable 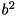$ b^2 $ is also updated according to 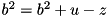$ b^2 = b^2 + u - z $ through ztilde.

Note: In most Gaussian noise restoration problems, the simpler d,u splitting algorithm is used (UseZ = 0). This routine is only needed in the special case of deconvolution with spatially-varying lambda.

static void ZSolvePoisson ( tvregsolver * S )

static

Solve the z-subproblem with a Poisson noise model.

Parameters

S	tvregsolver state

Solves the z-subproblem with Poisson noise model to update z,

$\operatorname*{arg\,min}_{z}\,\lambda\sum_{i,j}(z_{i,j} - f_{i,j}\log z_{i,j})+\frac{\gamma_2}{2}\sum_{i,j}(z_{i,j}-u_{i,j}-b^2_{i,j})^2,$

The auxiliary variable 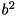$ b^2 $ is also updated according to 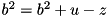$ b^2 = b^2 + u - z $ through ztilde.

Functions

Detailed Description

Function Documentation