Macros | |
| #define | init_randmt(seed) (init_randmt_r(&__randmt_global_generator, seed)) |
| Initialize the global generator with a seed. More... | |
| #define | init_randmt_auto() (init_randmt_auto_r(&__randmt_global_generator)) |
| Initialize the global generator with the current time. More... | |
| #define | rand_uint32() (rand_uint32_r(&__randmt_global_generator)) |
| Generate a random 32-bit unsigned integer (nonreentrant) More... | |
| #define | rand_unif() (rand_unif_r(&__randmt_global_generator)) |
| Generate a uniform random number on (0,1) (nonreentrant) More... | |
| #define | rand_normal() (rand_normal_r(&__randmt_global_generator)) |
| Generate a standard normal distributed random number (nonreentrant) More... | |
| #define | rand_exp(mu) (rand_exp_r(&__randmt_global_generator, mu)) |
| Generate an exponentially-distributed number (nonreentrant) More... | |
| #define | rand_gamma(a, b) (rand_gamma_r(&__randmt_global_generator, a, b)) |
| Generate a Gamma-distributed number (nonreentrant) More... | |
| #define | rand_poisson(mu) (rand_poisson_r(&__randmt_global_generator, mu)) |
| Generate a Poisson-distributed number (nonreentrant) More... | |
| #define | rand_geometric(p) (rand_geometric_r(&__randmt_global_generator, p)) |
| Generate a geometrically-distributed number (nonreentrant) More... | |
Detailed Description
These functions use the global pseudorandom number generator.
Macro Definition Documentation
| #define init_randmt | ( | seed | ) | (init_randmt_r(&__randmt_global_generator, seed)) |
Initialize the global generator with a seed.
- Parameters
-
seed the seed value
- See Also
- init_randmt_auto()
- init_randmt_r()
This routine seeds the global random number generator with an unsigned 32-bit integer value.
A constant seed can be used to reproduce the same pseudorandom numbers.
| #define init_randmt_auto | ( | ) | (init_randmt_auto_r(&__randmt_global_generator)) |
Initialize the global generator with the current time.
- See Also
- init_randmt()
- init_randmt_auto_r()
This function seeds the global generator with the current time. It should be called once at the beginning of the program so that different pseudorandom values are produced on different runs.
This function only needs to be called once. Seeding multiple times does not improve the statistical quality of the generator.
| #define rand_exp | ( | mu | ) | (rand_exp_r(&__randmt_global_generator, mu)) |
Generate an exponentially-distributed number (nonreentrant)
- Parameters
-
mu mean parameter of the distribution (positive value)
- Returns
- Pseudo-random exponentially-distibuted value with mean mu
- See Also
- rand_exp_r()
Generates a pseudo-random value distributed with probability density
![\[ f(x;\mu) = \begin{cases} \frac{1}{\mu} \mathrm{e}^{-x/\mu}, & x \ge 0, \\ 0, & x < 0, \end{cases} \]](form_16.png)
generated by inversion. The global generator is used to generate the value.
Distribution properties:
- CDF:
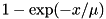
- Mean:
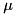
- Variance:
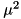
| #define rand_gamma | ( | a, | |
| b | |||
| ) | (rand_gamma_r(&__randmt_global_generator, a, b)) |
Generate a Gamma-distributed number (nonreentrant)
- Parameters
-
a shape parameter (positive value) b scale parameter (positive value)
- Returns
- Pseudo-random Gamma-distibuted value
- See Also
- rand_gamma_r()
Generates a Gamma-distributed random value with density
![\[ f(x;a,b) = x^{a-1} \frac{\exp(-x/b)}{\Gamma(a)b^k}, \quad x \ge 0, \]](form_20.png)
where 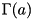 is the Gamma function, using the method of Marsaglia and Tsang, 2000. The global generator is used to generate the value.
is the Gamma function, using the method of Marsaglia and Tsang, 2000. The global generator is used to generate the value.
Distribution properties:
- CDF:
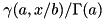 , where
, where 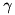 is the lower incomplete gamma function
is the lower incomplete gamma function - Mean:
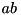
- Variance:
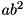
| #define rand_geometric | ( | p | ) | (rand_geometric_r(&__randmt_global_generator, p)) |
Generate a geometrically-distributed number (nonreentrant)
- Parameters
-
p probability of success
- Returns
- Pseudo-random geometrically-distibuted value
- See Also
- rand_geometric_r()
Generates a pseudo-random value distributed with probability mass fuction
![\[ \mathrm{P}(X = k) = (1 - p)^{k-1} p, \quad k = 1, 2, \ldots, \]](form_28.png)
where 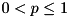 , generated by inversion. The global generator is used to generate the value.
, generated by inversion. The global generator is used to generate the value.
Distribution properties:
- CDF:
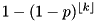
- Mean:
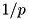
- Variance:
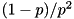
| #define rand_normal | ( | ) | (rand_normal_r(&__randmt_global_generator)) |
Generate a standard normal distributed random number (nonreentrant)
- Returns
- Pseudo-random double value with standard normal distribution
- See Also
- rand_normal_r()
A pseudo-random normally distributed number with density
![\[ f(x) = \frac{1}{\sqrt{2\pi}} \mathrm{e}^{-x^2/2}, \]](form_14.png)
generated by the Box-Muller transform. The global generator is used to generate the value.
Distribution properties:
- CDF:
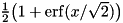
- Mean: 0
- Variance: 1
| #define rand_poisson | ( | mu | ) | (rand_poisson_r(&__randmt_global_generator, mu)) |
Generate a Poisson-distributed number (nonreentrant)
- Parameters
-
mu the mean parameter of the distribution (positive value)
- Returns
- Pseudo-random Poisson-distibuted value
- See Also
- rand_poisson_r()
A pseudo-random normally distributed number with probability mass function
![\[ \mathrm{P}(X = k) = \frac{\mu^k \mathrm{e}^{-\mu}}{k!}, \quad k = 0, 1,\ldots, \]](form_26.png)
using a simple direct algorthm for mu < 10 and the "PTRS" algorthm of Hormann for larger mu. The global generator is used to generate the value.
Reference: Wolfgang Hormann, "The transformed rejection method for generating Poisson random variables," Insurance: Mathematics and Economics 12, pp. 39-45, 1993.
Distribution properties:
- CDF:
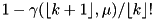 , where
, where 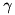 is the lower incomplete Gamma function
is the lower incomplete Gamma function - Mean:
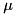
- Variance:
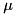
| #define rand_uint32 | ( | ) | (rand_uint32_r(&__randmt_global_generator)) |
Generate a random 32-bit unsigned integer (nonreentrant)
- Returns
- Pseudo-random integer value uniformly between 0 and 0xFFFFFFFF
- See Also
- rand_uint32_r()
- rand_unif()
The global generator is used to generate the value.
| #define rand_unif | ( | ) | (rand_unif_r(&__randmt_global_generator)) |
Generate a uniform random number on (0,1) (nonreentrant)
- Returns
- Pseudo-random double value in the open interval (0,1)
- See Also
- rand_unif_r()
- rand_uint32()
This routine generates a random number uniformly on the open interval (0,1) with 53-bit resolution. The formula used to generate the number is
![\[ \mathtt{rand\_unif} = (a 2^{26} + b + 0.5 - \epsilon) / 2^{53}, \]](form_10.png)
where a = integer of 27 random bits, b = integer of 26 random bits. The global generator is used to generate the value.
Distribution properties:
- CDF:
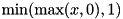
- Mean:
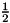
- Variance:
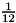
 1.8.3.1
1.8.3.1