Solve the d subproblem. More...
#include "tvregopt.h"Go to the source code of this file.
Functions | |
| static void | DSolve (tvregsolver *S) |
| Solve the d subproblem with vectorial shrinkage. More... | |
Detailed Description
Solve the d subproblem.
Copyright (c) 2010-2012, Pascal Getreuer All rights reserved.
This program is free software: you can use, modify and/or redistribute it under the terms of the simplified BSD License. You should have received a copy of this license along this program. If not, see http://www.opensource.org/licenses/bsd-license.html.
Definition in file dsolve_inc.c.
Function Documentation
|
static |
Solve the d subproblem with vectorial shrinkage.
- Parameters
-
S tvreg solver state
This routine solves the d subproblem to update d,
![\[ \operatorname*{arg\,min}_{d}\,\sum_{i,j}\lvert d_{i,j}\rvert+\frac{ \gamma}{2}\sum_{i,j}\lvert d_{i,j}-b_{i,j}-\nabla u_{i,j}\rvert^2, \]](form_0.png)
where 
is the discrete gradient and the second term is a penalty to encourage the constraint 
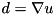. The solution is the vectorial shrinkage with shrinkage parameter 
,
![\[ d_{i,j}=\frac{\nabla u_{i,j}+b_{i,j}}{\lvert\nabla u_{i,j}+b_{i,j} \rvert}\max\bigl\{\lvert\nabla u_{i,j}+b_{i,j}\rvert-1/\gamma,0\bigr\}. \]](form_4.png)
The discrete gradient of u is computed with forward differences. At the right and bottom boundaries, the difference is set to zero.
The routine also updates the auxiliary variable b according to
![\[ b = b + \nabla u - d. \]](form_5.png)
Rather than representing b directly, we use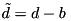 
, which is algebraically equivalent but requires less arithmetic.
To represent the vector field d, we implement d as a numvec2 array of size Width x Height x NumChannels such that
where i = 0, ..., Width-1, j = 0, ..., Height-1, and k = 0, ..., NumChannels-1. This structure is also used for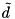 
.
Definition at line 47 of file dsolve_inc.c.
