u-subproblem Gauss-Seidel solvers for denoising and inpainting More...
Go to the source code of this file.
Functions | |
| static num | UGaussSeidelConstantLambda (tvregsolver *S) |
| Approximately solve the u-subproblem for constant lambda. More... | |
| static num | UGaussSeidelVaryingLambda (tvregsolver *S) |
| Approximately solve the u-subproblem for varying lambda. More... | |
Detailed Description
u-subproblem Gauss-Seidel solvers for denoising and inpainting
Copyright (c) 2010-2012, Pascal Getreuer All rights reserved.
This program is free software: you can use, modify and/or redistribute it under the terms of the simplified BSD License. You should have received a copy of this license along this program. If not, see http://www.opensource.org/licenses/bsd-license.html.
Definition in file usolve_gs_inc.c.
Function Documentation
|
static |
Approximately solve the u-subproblem for constant lambda.
- Parameters
-
S tvreg solver state
Performs one Gauss-Seidel iteration on u to improve the solution in the u-subproblem for denoising problems with constant lambda,
![\[ \alpha u-\Delta u=\alpha\tilde{z}-\operatorname{div}\tilde{d}, \]](form_33.png)
where 
, 
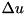is the discrete Laplacian of u, and 
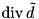is the discrete divergence of dtilde.
In the interior domain, the Gauss-Seidel update is
![\[ u_{i,j}=\frac{\alpha\tilde{z}_{i,j}-\tilde{d}^x_{i,j}+ \tilde{d}^x_{i-1,j}-\tilde{d}^y_{i,j} + \tilde{d}^y_{i,j-1}+u_{i-1,j} +u_{i+1,j}+u_{i,j-1}+u_{i,j+1}}{\alpha+4}. \]](form_37.png)
|
static |
Approximately solve the u-subproblem for varying lambda.
- Parameters
-
S tvreg solver state
This function is used for problems where there is no deconvolution and spatially-varying lambda, e.g., pure inpainting problems. It is the same as UGaussSeidelConstantLambda() except that lambda is spatially varying.
