DGtal  0.6.devel
 All Data Structures Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Groups Pages
Data Structures | Public Types | Public Member Functions | Data Fields | Protected Attributes | Private Member Functions
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity > Class Template Reference

#include <ArithmeticalDSS.h>

Inheritance diagram for DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >:
Inheritance graph
[legend]
Collaboration diagram for DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >:
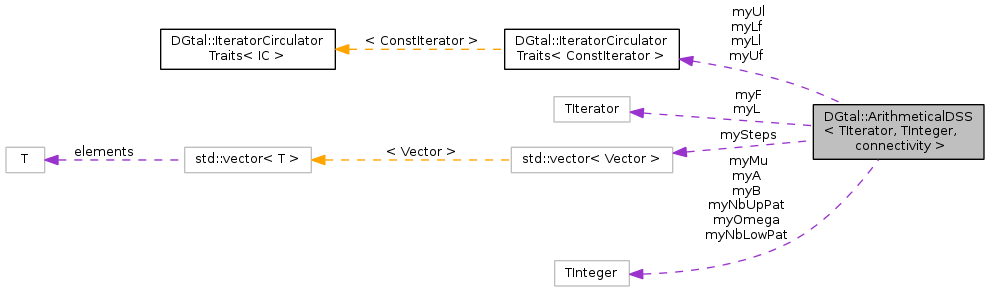
Collaboration graph
[legend]

Data Structures

struct  Tools
struct  Tools< TInt, 4 >

Public Types

typedef TInteger Integer
typedef TIterator ConstIterator
typedef ArithmeticalDSS
< ConstIterator, TInteger,
connectivity > 		Self
typedef ArithmeticalDSS
< ReverseIterator
< ConstIterator >, TInteger,
connectivity > 		Reverse
typedef
IteratorCirculatorTraits
< ConstIterator >::Value 		Point
typedef
IteratorCirculatorTraits
< ConstIterator >::Value 		Vector
typedef PointVector< 2, double > PointD

Public Member Functions

 BOOST_CONCEPT_ASSERT ((CInteger< TInteger >))
 BOOST_STATIC_ASSERT ((Point::dimension==2))
 ArithmeticalDSS ()
 ArithmeticalDSS (const ConstIterator &it)
void init (const ConstIterator &it)
 ArithmeticalDSS (const Self &other)
Self & operator= (const Self &other)
Self getSelf () const
Reverse getReverse () const
bool operator== (const Self &other) const
bool operator!= (const Self &other) const
 ~ArithmeticalDSS ()
bool isExtendableForward (const ConstIterator &itf)
bool isExtendableForward ()
bool isExtendableBackward ()
bool extendForward (const ConstIterator &itf)
bool extendBackward (const ConstIterator &itb)
bool extendForward ()
bool extendBackward ()
bool retractForward ()
bool retractBackward ()
Integer getA () const
Integer getB () const
Integer getMu () const
Integer getOmega () const
Point getUf () const
Point getUl () const
Point getLf () const
Point getLl () const
Point getBackPoint () const
Point getFrontPoint () const
Point getFirstPoint () const
Point getLastPoint () const
ConstIterator getBack () const
ConstIterator getFront () const
ConstIterator begin () const
ConstIterator end () const
bool isValid () const
Integer getRemainder (const ConstIterator &it) const
Integer getRemainder (const Point &aPoint) const
Integer getPosition (const ConstIterator &it) const
Integer getPosition (const Point &aPoint) const
bool isInDSL (const Point &aPoint) const
bool isInDSL (const ConstIterator &it) const
bool isInDSS (const Point &aPoint) const
bool isInDSS (const ConstIterator &it) const
PointD project (const Point &m) const
PointD project (const Point &m, double r) const
PointD project (const Point &m, const Point &p) const
double projectedSegmentLength () const
void selfDisplay (std::ostream &out)
std::string className () const

Data Fields

Point myUf
Point myUl
Point myLf
Point myLl
ConstIterator myF
ConstIterator myL

Protected Attributes

Integer myA
Integer myB
Integer myMu
Integer myOmega
Integer myNbUpPat
Integer myNbLowPat
std::vector< Vector > mySteps

Private Member Functions

bool isExtendableForward (const Point &lastPoint, const Vector &lastMove)
bool extendForward (const ConstIterator &it, ConstIterator &lastIt, const Vector &lastMove, Point &Uf, Point &Ul, Point &Lf, Point &Ll)
bool retractForward (ConstIterator &firstIt, ConstIterator &lastIt, ConstIterator &nextIt, Point &Uf, Point &Ul, Point &Lf, Point &Ll, const Integer &s)
bool hasLessThanTwoSteps (const Vector &aStep) const
Vector vectorFrom0ToOmega () const

Detailed Description

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
class DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >

Aim: Dynamic recognition of a digital straight segment (DSS) defined as the sequence of simply connected points (x,y) such that mu <= ax - by < mu + omega. 

 Description of class 'ArithmeticalDSS' <p>
 @note I. DEBLED-RENNESSON, J.-P. REVEILLES, 
 A linear algorithm for segmentation of digital curves, 
 International Journal of Pattern Recognition and Artificial
 Intelligence, Volume 9, N. 6, December 1995. 

 This class is a model of the concept CDynamicBidirectionalSegmentComputer. 

 Here is a short example of how to use this class:
 @snippet geometry/curves/ArithmeticalDSS.cpp ArithmeticalDSS4Usage

 You must get: 

 @code

[ArithmeticalDSS] Parameters (a,b,mu,omega)=(2, 5, -4, 7) Number of upper patterns: 0 Number of lower patterns: 1 First point [PointVector] {0, 0} Last point [PointVector] {6, 3} Leaning points: Uf [PointVector] {3, 2} Ul [PointVector] {3, 2} Lf [PointVector] {1, 0} Ll [PointVector] {6, 2} Steps: [PointVector] {1, 0} [PointVector] {0, 1} [End ArithmeticalDSS]

Template Parameters:
'TIterator'type ConstIterator on 2D points,
'TInteger'type of scalars used for the DSS parameters (satisfying CInteger)
'connectivity'an integer equal to 4 for standard (4-connected) DSS or 8 for naive (8-connected) DSS. (Any other integers act as 8).
See also:
ArithmeticalDSS.cpp testArithDSS.cpp

Definition at line 116 of file ArithmeticalDSS.h.

Member Typedef Documentation

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
typedef TIterator DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::ConstIterator

Definition at line 201 of file ArithmeticalDSS.h.

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
typedef TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Integer

Definition at line 198 of file ArithmeticalDSS.h.

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
typedef IteratorCirculatorTraits<ConstIterator>::Value DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point

Definition at line 206 of file ArithmeticalDSS.h.

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
typedef PointVector<2,double> DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::PointD

Definition at line 214 of file ArithmeticalDSS.h.

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
typedef ArithmeticalDSS<ReverseIterator<ConstIterator>,TInteger,connectivity> DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Reverse

Definition at line 203 of file ArithmeticalDSS.h.

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
typedef ArithmeticalDSS<ConstIterator,TInteger,connectivity> DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Self

Definition at line 202 of file ArithmeticalDSS.h.

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
typedef IteratorCirculatorTraits<ConstIterator>::Value DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Vector

Definition at line 207 of file ArithmeticalDSS.h.

Constructor & Destructor Documentation

template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::ArithmeticalDSS ( )
inline

Default constructor. not valid

Definition at line 48 of file ArithmeticalDSS.ih.

{
myUf = Point(0,0);
myLf = Point(0,0);
myUl = Point(0,0);
myLl = Point(0,0);
myA = 0;
myB = 0;
myMu = 0;
myOmega = 0;
myNbUpPat = 0;
myNbLowPat = 0;
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::ArithmeticalDSS ( const ConstIterator &  it)
inline

Constructor with initialisation

Parameters:
itan iterator on 2D points
See also:
init

Definition at line 66 of file ArithmeticalDSS.ih.

{
init(it);
}
template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::ArithmeticalDSS ( const Self &  other)

Copy constructor.

Parameters:
otherthe object to clone.
template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::~ArithmeticalDSS ( )
inline

Destructor.

Definition at line 286 of file ArithmeticalDSS.h.

{};

Member Function Documentation

template<typename TIterator , typename TInteger , int connectivity>
TIterator DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::begin ( ) const
inline
Returns:
begin iterator of the DSS range.

Definition at line 887 of file ArithmeticalDSS.ih.

{
return myF;
}
template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::BOOST_CONCEPT_ASSERT ( (CInteger< TInteger >)  )
template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::BOOST_STATIC_ASSERT ( (Point::dimension==2)  )
template<typename TIterator , typename TInteger , int connectivity>
std::string DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::className ( ) const
inline

Default drawing style object.

Parameters:
modethe drawing mode.
Returns:
the dyn. alloc. default style for this object.
the style name used for drawing this object.

Definition at line 1002 of file ArithmeticalDSS.ih.

Referenced by DGtal::Display2DFactory::draw().

{
return "ArithmeticalDSS";
}
template<typename TIterator , typename TInteger , int connectivity>
TIterator DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::end ( ) const
inline
Returns:
end iterator of the DSS range.

Definition at line 894 of file ArithmeticalDSS.ih.

{
ConstIterator i(myL); ++i;
return i;
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::extendBackward ( const ConstIterator &  itb)
inline
Deprecated:
See also:
extendBackward()

Tests whether the union between a point (adding to the back of the DSS with respect to the scan orientaion) and a DSS is a DSS. Computes the parameters of the new DSS with the adding point if true.

Parameters:
itban iterator on a sequence of points
Returns:
'true' if the union is a DSS, 'false' otherwise.

Definition at line 356 of file ArithmeticalDSS.ih.

Referenced by DGtal::FP< TIterator, TInteger, connectivity >::FP().

{
return extendForward(it, myF, (Point(*myF) - Point(*it)), myUl, myUf, myLl, myLf);
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::extendBackward ( )
inline

Tests whether the current DSS can be extended at the back. Computes the parameters of the extended DSS if yes.

Returns:
'true' if yes, 'false' otherwise.

Definition at line 380 of file ArithmeticalDSS.ih.

{
ConstIterator it(myF); --it;
return extendForward(it, myF, (Point(*myF) - Point(*it)), myUl, myUf, myLl, myLf);
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::extendForward ( const ConstIterator &  itf)
inline
Deprecated:
See also:
extendForward()

Tests whether the union between a point (adding to the front of the DSS with respect to the scan orientaion) and a DSS is a DSS. Computes the parameters of the new DSS with the adding point if true.

Parameters:
itfan iterator on a sequence of points
Returns:
'true' if the union is a DSS, 'false' otherwise.

Definition at line 344 of file ArithmeticalDSS.ih.

Referenced by DGtal::FP< TIterator, TInteger, connectivity >::FP().

{
return extendForward(it, myL, (Point(*it) - Point(*myL)), myUf, myUl, myLf, myLl);
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::extendForward ( )
inline

Tests whether the current DSS can be extended at the front. Computes the parameters of the extended DSS if yes.

Returns:
'true' if yes, 'false' otherwise.

Definition at line 368 of file ArithmeticalDSS.ih.

{
ConstIterator it(myL); ++it;
return extendForward(it, myL, (Point(*it) - Point(*myL)), myUf, myUl, myLf, myLl);
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::extendForward ( const ConstIterator &  it,
ConstIterator &  lastIt,
const Vector &  lastMove,
Point &  Uf,
Point &  Ul,
Point &  Lf,
Point &  Ll 
)
inlineprivate

Tests whether the union between a point (pointing to by it) and the DSS is a DSS. Computes the parameters of the new DSS with the adding point if true.

Parameters:
itan iterator on a 2D point
lastItan iterator pointing to the end of the DSS
lastMoveshift vector to the point pointed to by it
Uffirst upper leaning point
Ullast upper leaning point
Lffirst lower leaning point
Lllast lower leaning point
Returns:
'true' if the union is a DSS, 'false' otherwise.

Definition at line 186 of file ArithmeticalDSS.ih.

{
Point lastPoint(*it);
Integer deviation = Tools<Integer,connectivity>
::norm(lastMove[0],lastMove[1]);
//if the two last points are not connected return false
if (deviation > NumberTraits<Integer>::ONE) return false;
//if the two last points are confounded return true
else if (deviation == NumberTraits<Integer>::ZERO)
{
//add the point to the DSS
lastIt = it;
return true;
}
//otherwise
else if (mySteps.size()<2) {
//initialisation stage
if (mySteps.size()==0) {
mySteps.push_back(lastMove);
//update
lastIt = it;
Ul = lastPoint;
Ll = lastPoint;
myA += lastMove[1];
myB += lastMove[0];
myMu = getRemainder(myUl);
myOmega = Tools<Integer,connectivity>::norm(myA,myB);
myNbUpPat = 1;
myNbLowPat = 1;
return true;
} else { //mySteps.size() == 1
if (lastMove == mySteps.at(0)) {
//update
lastIt = it;
Ul = lastPoint;
Ll = lastPoint;
myNbUpPat++;
myNbLowPat++;
return true;
} else {
//difference of the two steps viewed as points
Vector diff = ( lastMove-mySteps.at(0) );
if (Tools<Integer,connectivity>::dualNorm(diff[0],diff[1]) == NumberTraits<Integer>::ONE) {
//the two steps are compatible
//update
lastIt = it;
//remainder
Integer r = getRemainder(lastPoint);
if ( r < myMu) { //on the left
Ul = lastPoint;
Lf = Ll;
myA = myNbUpPat*mySteps.at(0)[1] + lastMove[1];
myB = myNbUpPat*mySteps.at(0)[0] + lastMove[0];
myNbUpPat = 1;
myNbLowPat = 0;
} else { //on the right
Ll = lastPoint;
Uf = Ul;
myA = myNbUpPat*mySteps.at(0)[1] + lastMove[1];
myB = myNbUpPat*mySteps.at(0)[0] + lastMove[0];
myNbUpPat = 0;
myNbLowPat = 1;
}
myMu = getRemainder(myUl);
myOmega = Tools<Integer,connectivity>::norm(myA,myB);
mySteps.push_back(lastMove);
return true;
} else { //the two steps are not compatible
return false;
}
}
}
} else { //mySteps.size() == 2
//main stage
//if there are only two steps at most
if (hasLessThanTwoSteps(lastMove)) {
//remainder
Integer r = getRemainder(lastPoint);
if ( (r < myMu-1)||(r > myMu+myOmega) )
return false; //strongly exterior
else {
//add the point to the DSS
lastIt = it;
//update
//if weakly interior
if (r == myMu) {
Ul = lastPoint;
myNbUpPat++;
}
if (r == myMu+myOmega-1) {
Ll = lastPoint;
myNbLowPat++;
}
//if weakly exterior
if (r == myMu-1) { //on the left
Ul = lastPoint;
Lf = Ll;
myA = myUl[1] - myUf[1];
myB = myUl[0] - myUf[0];
myMu = getRemainder(myUl);
myOmega = Tools<Integer,connectivity>::norm(myA,myB);
myNbUpPat = 1;
myNbLowPat = 0;
} else if (r == myMu+myOmega) { //on the right
Ll = lastPoint;
Uf = Ul;
myA = myLl[1] - myLf[1];
myB = myLl[0] - myLf[0];
myMu = getRemainder(myUl);
myOmega = Tools<Integer,connectivity>::norm(myA,myB);
myNbUpPat = 0;
myNbLowPat = 1;
}
return true;
}
} else {
//if there is more than two steps
return false;
}
}
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getA ( ) const
inline
Returns:
an Integer of value myA.

Definition at line 790 of file ArithmeticalDSS.ih.

{
return myA;
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getB ( ) const
inline
Returns:
an Integer of value myB.

Definition at line 797 of file ArithmeticalDSS.ih.

{
return myB;
}
template<typename TIterator , typename TInteger , int connectivity>
TIterator DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getBack ( ) const
inline
Deprecated:
See also:
begin() end()

Accessor to the iterator at the back of the DSS

Returns:
iterator pointing to the back of the DSS.

Definition at line 873 of file ArithmeticalDSS.ih.

{
return myF;
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getBackPoint ( ) const
inline
Deprecated:
Accessor to the first added point to the DSS
Returns:
the first point of the DSS.

Definition at line 845 of file ArithmeticalDSS.ih.

{
return (*myF);
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getFirstPoint ( ) const
inline

Accessor to the first added point to the DSS

Returns:
the first point of the DSS.

Definition at line 859 of file ArithmeticalDSS.ih.

{
return (*myF);
}
template<typename TIterator , typename TInteger , int connectivity>
TIterator DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getFront ( ) const
inline
Deprecated:
See also:
begin() end()

Accessor to the iterator at the front of the DSS

Returns:
iterator pointing to the front of the DSS.

Definition at line 880 of file ArithmeticalDSS.ih.

{
return myL;
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getFrontPoint ( ) const
inline
Deprecated:
Accessor to the last added point to the DSS
Returns:
the last point of the DSS.

Definition at line 852 of file ArithmeticalDSS.ih.

{
return (*myL);
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getLastPoint ( ) const
inline

Accessor to the last added point to the DSS

Returns:
the last point of the DSS.

Definition at line 866 of file ArithmeticalDSS.ih.

{
return (*myL);
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getLf ( ) const
inline

Accessor to the first lower leaning point

Returns:
first lower leaning point.

Definition at line 831 of file ArithmeticalDSS.ih.

Referenced by DGtal::Adapter4ConcavePart< ArithmeticalDSS >::firstLeaningPoint(), and DGtal::FP< TIterator, TInteger, connectivity >::FP().

{
return myLf;
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getLl ( ) const
inline

Accessor to the last lower leaning point

Returns:
last lower leaning point.

Definition at line 838 of file ArithmeticalDSS.ih.

Referenced by DGtal::Adapter4ConcavePart< ArithmeticalDSS >::lastLeaningPoint().

{
return myLl;
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getMu ( ) const
inline
Returns:
an Integer of value myMu.

Definition at line 804 of file ArithmeticalDSS.ih.

{
return myMu;
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getOmega ( ) const
inline
Returns:
an Integer of value myOmega.

Definition at line 811 of file ArithmeticalDSS.ih.

{
return myOmega;
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getPosition ( const ConstIterator &  it) const
inline

Computes the position of a point (that does not necessarily belong to the DSS)

Parameters:
itan iterator on points
Returns:
the position of *it.

Definition at line 739 of file ArithmeticalDSS.ih.

{
return getPosition(*it);
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getPosition ( const Point &  aPoint) const
inline

Computes the position of a point (that does not necessarily belong to the DSS)

Parameters:
aPointthe point whose position is returned
Returns:
myA * aPoint[0] + myB * aPoint[1].

Definition at line 730 of file ArithmeticalDSS.ih.

{
return myA * static_cast<Integer>(aPoint[0])
+ myB * static_cast<Integer>(aPoint[1]);
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getRemainder ( const ConstIterator &  it) const
inline

Computes the remainder of a point (that does not necessarily belong to the DSS)

Parameters:
itan iterator on points
Returns:
the remainder of *it.

Definition at line 721 of file ArithmeticalDSS.ih.

{
return getRemainder(*it);
}
template<typename TIterator , typename TInteger , int connectivity>
TInteger DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getRemainder ( const Point &  aPoint) const
inline

Computes the remainder of a point (that does not necessarily belong to the DSS)

Parameters:
aPointthe point whose remainder is returned
Returns:
myA * aPoint[0] - myB * aPoint[1].

Definition at line 711 of file ArithmeticalDSS.ih.

{
return myA * static_cast<Integer>(aPoint[0])
- myB * static_cast<Integer>(aPoint[1]);
}
template<typename TIterator , typename TInteger , int connectivity>
ArithmeticalDSS< TIterator, TInteger, connectivity >::Reverse DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getReverse ( ) const
inline
Returns:
a default-constructed instance of Reverse

Definition at line 138 of file ArithmeticalDSS.ih.

{
return Reverse();
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Self DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getSelf ( ) const
inline
Returns:
a default-constructed instance of Self

Definition at line 146 of file ArithmeticalDSS.ih.

{
return Self();
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getUf ( ) const
inline

Accessor to the first upper leaning point

Returns:
first upper leaning point.

Definition at line 818 of file ArithmeticalDSS.ih.

Referenced by DGtal::Adapter4ConvexPart< ArithmeticalDSS >::firstLeaningPoint(), and DGtal::FP< TIterator, TInteger, connectivity >::FP().

{
return myUf;
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::getUl ( ) const
inline

Accessor to the last upper leaning point

Returns:
last upper leaning point.

Definition at line 824 of file ArithmeticalDSS.ih.

Referenced by DGtal::Adapter4ConvexPart< ArithmeticalDSS >::lastLeaningPoint().

{
return myUl;
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::hasLessThanTwoSteps ( const Vector &  aStep) const
inlineprivate

Checks whether the DSS has less or more than two shift vectors (steps) between two consecutive points (must be called only in the main stage)

Parameters:
aStepthe last shift vector.
Returns:
'true' if less or equal, 'false' otherwise.

Definition at line 1040 of file ArithmeticalDSS.ih.

{
if ( (aStep == mySteps.at(0)) ||
(aStep == mySteps.at(1)) ) {
return true;
} else {
return false;
}
}
template<typename TIterator , typename TInteger , int connectivity>
void DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::init ( const ConstIterator &  it)
inline

Initialisation.

Parameters:
itan iterator on 2D points

Definition at line 73 of file ArithmeticalDSS.ih.

{
myF = it;
myL = it;
myUf = *it;
myLf = *it;
myUl = *it;
myLl = *it;
myA = 0;
myB = 0;
myMu = 0;
myOmega = 0;
myNbUpPat = 0;
myNbLowPat = 0;
mySteps.clear();
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isExtendableBackward ( )
inline

Tests whether the current DSS can be extended at the back.

Returns:
'true' if yes, 'false' otherwise.

Definition at line 628 of file ArithmeticalDSS.ih.

{
ConstIterator it(myF); --it;
return isExtendableForward(*it, (Point(*myF) - Point(*it)) );
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isExtendableForward ( const ConstIterator &  itf)
inline
Deprecated:
See also:
isExtendableForward()

Tests whether the union between a point (adding to the front of the DSS with respect to the scan orientaion) and a DSS is a DSS.

Parameters:
itfan iterator on a sequence of points
Returns:
'true' if the union is a DSS, 'false' otherwise.

Definition at line 543 of file ArithmeticalDSS.ih.

{
Point lastPoint(*it);
Vector lastMove = lastPoint-Point(*myL);
Integer deviation = Tools<Integer,connectivity>
::norm(lastMove[0],lastMove[1]);
//if the two last points are not connected return false
if (deviation>NumberTraits<Integer>::ONE) return false;
//if the two last points are confounded return true
else if (deviation==NumberTraits<Integer>::ZERO) return true;
//otherwise
else if (mySteps.size()<2) {
//initialisation stage
if (mySteps.size()==0) {
return true;
} else { //mySteps.size() == 1
if (lastMove == mySteps.at(0)) {
return true;
} else {
//difference of the two steps viewed as points
Vector diff = ( lastMove-mySteps.at(0) );
if (Tools<Integer,connectivity>::dualNorm(diff[0],diff[1]) == NumberTraits<Integer>::ONE) {
//the two steps are compatible
return true;
} else { //the two steps are not compatible
return false;
}
}
}
} else { //mySteps.size() == 2
//main stage
//if there only two steps at most
if (hasLessThanTwoSteps(lastMove)) {
//remainder
Integer r = getRemainder(lastPoint);
if ( (r < myMu-1)||(r > myMu+myOmega) )
return false; //strongly exterior
else {
return true;
}
} else {
//if there is more than two steps
return false;
}
}
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isExtendableForward ( )
inline

Tests whether the current DSS can be extended at the front.

Returns:
'true' if yes, 'false' otherwise.

Definition at line 616 of file ArithmeticalDSS.ih.

{
ConstIterator it(myL); ++it;
return isExtendableForward(*it, (Point(*it) - Point(*myL)) );
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isExtendableForward ( const Point &  lastPoint,
const Vector &  lastMove 
)
inlineprivate

Tests whether the union between lastPoint and the DSS is a DSS. Computes the parameters of the new DSS with the adding point if true.

Parameters:
lastPointthe point to add
lastMoveshift vector to the point to add
Returns:
'true' if the union is a DSS, 'false' otherwise.

Definition at line 639 of file ArithmeticalDSS.ih.

{
Integer deviation = Tools<Integer,connectivity>
::norm(lastMove[0],lastMove[1]);
//if the two last points are not connected return false
if (deviation > NumberTraits<Integer>::ONE) return false;
//if the two last points are confounded return true
else if (deviation == NumberTraits<Integer>::ZERO) return true;
//otherwise
else if (mySteps.size()<2) {
//initialisation stage
if (mySteps.size()==0) {
return true;
} else { //mySteps.size() == 1
if (lastMove == mySteps.at(0)) {
return true;
} else {
//difference of the two steps viewed as points
Vector diff = ( lastMove-mySteps.at(0) );
if (Tools<Integer,connectivity>::dualNorm(diff[0],diff[1]) == 1) {
//the two steps are compatible
return true;
} else { //the two steps are not compatible
return false;
}
}
}
} else { //mySteps.size() == 2
//main stage
//if there only two steps at most
if (hasLessThanTwoSteps(lastMove)) {
//remainder
Integer r = getRemainder(lastPoint);
if ( (r < myMu-1)||(r > myMu+myOmega) )
return false; //strongly exterior
else
return true;
} else {
//if there is more than two steps
return false;
}
}
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isInDSL ( const Point &  aPoint) const
inline

Checks whether a point is in the DSL of parameters ( myA, myB, myMu, myOmega )

Parameters:
aPointthe point to be checked
Returns:
'true' if yes, 'false' otherwise

Definition at line 748 of file ArithmeticalDSS.ih.

{
Integer r = getRemainder(aPoint);
return ( (r >= myMu)&&(r < myMu+myOmega) );
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isInDSL ( const ConstIterator &  it) const
inline

Checks whether a point is in the DSL of parameters ( myA, myB, myMu, myOmega )

Parameters:
itan iterator on the point to be checked
Returns:
'true' if yes, 'false' otherwise

Definition at line 758 of file ArithmeticalDSS.ih.

{
return isInDSL(*it);
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isInDSS ( const Point &  aPoint) const
inline

Checks whether a point belongs to the DSS or not

Parameters:
aPointthe point to be checked
Returns:
'true' if yes, 'false' otherwise

Definition at line 767 of file ArithmeticalDSS.ih.

{
Integer s = getPosition(aPoint);
Integer smin = getPosition(myF);
Integer smax = getPosition(myL);
return (isInDSL(aPoint) && ( (s >= smin)&&(s <= smax) ) );
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isInDSS ( const ConstIterator &  it) const
inline

Checks whether a point belongs to the DSS or not

Parameters:
itan iterator on the point to be checked
Returns:
'true' if yes, 'false' otherwise

Definition at line 779 of file ArithmeticalDSS.ih.

{
return isInDSS(*it);
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::isValid ( ) const
inline

Checks the validity/consistency of the object.

Returns:
'true' if the object is valid, 'false' otherwise.

Definition at line 903 of file ArithmeticalDSS.ih.

{
if (Point(*myF) == Point(*myL)) {
//init case with one point
if ( (myA==0)
&&(myB==0)
&&(myMu==0)
&&(myOmega==0)
&&(myNbUpPat==0)
&&(myNbLowPat==0) ) return true;
else return false;
} else {
//remainders of leaning points
if (getRemainder(myUf) != myMu) return false;
else if (getRemainder(myUl) != myMu) return false;
else if (getRemainder(myLf) != myMu+myOmega-1) return false;
else if (getRemainder(myLl) != myMu+myOmega-1) return false;
//number of patterns
else if ( (Vector(myB,myA)*myNbUpPat) != (myUl - myUf) ) return false;
else if ( (Vector(myB,myA)*myNbLowPat) != (myLl - myLf) ) return false;
else return true;
}
}
template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator!= ( const Self &  other) const
inline

Difference operator.

Parameters:
otherthe object to compare with.
Returns:
'false' if equal 'true' otherwise

Definition at line 176 of file ArithmeticalDSS.ih.

{
return (!(*this == other));
}
template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Self & DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator= ( const Self &  other)
inline

Assignment.

Parameters:
otherthe object to copy.
Returns:
a reference on 'this'.

Definition at line 112 of file ArithmeticalDSS.ih.

References DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myA, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myB, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myF, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myL, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myLf, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myLl, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myMu, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myNbLowPat, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myNbUpPat, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myOmega, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::mySteps, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myUf, and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myUl.

{
if ( this != &other )
{
myA = other.myA;
myB = other.myB;
myMu = other.myMu;
myOmega = other.myOmega;
myNbUpPat = other.myNbUpPat;
myNbLowPat = other.myNbLowPat;
myUf = other.myUf;
myLf = other.myLf;
myUl = other.myUl;
myLl = other.myLl;
myF = other.myF;
myL = other.myL;
mySteps = other.mySteps;
}
return *this;
}
template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator== ( const Self &  other) const
inline

Equality operator.

Parameters:
otherthe object to compare with.
Returns:
'true' either if the leaning points perfectly match or if the first leaning points match to the last ones (same DSS scanned in the reverse way) and 'false' otherwise

Definition at line 155 of file ArithmeticalDSS.ih.

References DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myF, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myL, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myLf, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myLl, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myOmega, DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myUf, and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myUl.

{
return ( ( (myOmega == other.myOmega) &&
(myUf == other.myUf) &&
(myUl == other.myUl) &&
(myLf == other.myLf) &&
(myLl == other.myLl) &&
(*myF == *other.myF) &&
(*myL == *other.myL) ) ||
( (myOmega == other.myOmega) &&
(myUf == other.myLl) &&
(myUl == other.myLf) &&
(myLf == other.myUl) &&
(myLl == other.myUf) &&
(*myF == *other.myL) &&
(*myL == *other.myF) ) );
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::PointD DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::project ( const Point &  m) const
inline

Projects the point m onto the straight line of slope ( myA / myB) and intercept myMu + ( myOmega - 1 )/2 ).

Parameters:
many point (may not be part of the DSS).
Returns:
the projected point.

Definition at line 938 of file ArithmeticalDSS.ih.

Referenced by DGtal::Display2DFactory::drawAsBoundingBox().

{
//casts
double a = (double) NumberTraits<TInteger>::castToInt64_t(myA);
double b = (double) NumberTraits<TInteger>::castToInt64_t(myB);
double mu = (double) NumberTraits<TInteger>::castToInt64_t(myMu);
double omega = (double) NumberTraits<TInteger>::castToInt64_t(myOmega);
double xm = (double) NumberTraits<TInteger>::castToInt64_t(m[0]);
double ym = (double) NumberTraits<TInteger>::castToInt64_t(m[1]);
double alpha = ( mu + (omega - 1.0)/2.0 );
double d2 = ( a * a + b * b );
double s = b * xm + a * ym;
double xp = ( b * s + a * alpha ) / d2;
double yp = ( a * s - b * alpha ) / d2;
return PointD( xp, yp );
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::PointD DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::project ( const Point &  m,
double  r 
) const
inline

Projects the point m onto the straight line whose points have remainder r.

Parameters:
many point (may not be part of the DSS).
rthe remainder (may not be an integer).
Returns:
the projected point.

Definition at line 959 of file ArithmeticalDSS.ih.

{
//casts
double a = (double) NumberTraits<TInteger>::castToInt64_t(myA);
double b = (double) NumberTraits<TInteger>::castToInt64_t(myB);
double xm = (double) NumberTraits<TInteger>::castToInt64_t(m[0]);
double ym = (double) NumberTraits<TInteger>::castToInt64_t(m[1]);
double d2 = ( a * a + b * b );
double s = b * xm + a * ym;
double xp = ( b * s + a * r ) / d2;
double yp = ( a * s - b * r ) / d2;
return PointD( xp, yp );
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::PointD DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::project ( const Point &  m,
const Point &  p 
) const
inline

Projects the point m onto the straight line going through point p.

Parameters:
many point (may not be part of the DSS).
pany point (may not be part of the DSS).
Returns:
the projected point.

Definition at line 979 of file ArithmeticalDSS.ih.

{
double r = (double) NumberTraits<TInteger>::castToInt64_t(getRemainder(p));
return project(m,r);
}
template<typename TIterator , typename TInteger , int connectivity>
double DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::projectedSegmentLength ( ) const
inline
Returns:
the projected length of the segment.

Definition at line 990 of file ArithmeticalDSS.ih.

References DGtal::PointVector< dim, TEuclideanRing >::norm().

{
PointD v = project( *myL );
PointD u = project( *myF );
v -= u;
return v.norm(PointD::L_2);
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::retractBackward ( )
inline

Removes the last point of the DSS (at front) if it has more than two points

Returns:
'true' if the last point is removed, 'false' otherwise.

Definition at line 526 of file ArithmeticalDSS.ih.

{
Vector v = Point(*myL)-Point(*myF);
if ( (v[0] == 0) && (v[1] == 0) ) {//if there is only one point
return false;
} else { //otherwise
ConstIterator previous(myL); --previous;
return retractForward(myL, myF, previous, myUl, myUf, myLl, myLf, -1);
}
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::retractForward ( )
inline

Removes the first point of the DSS (at back) if it has more than two points

Returns:
'true' if the first point is removed, 'false' otherwise.

Definition at line 509 of file ArithmeticalDSS.ih.

{
Vector v = Point(*myL)-Point(*myF);
if ( (v[0] == 0) && (v[1] == 0) ) {//if there is only one point
return false;
} else { //otherwise
ConstIterator next(myF); ++next;
return retractForward(myF, myL, next, myUf, myUl, myLf, myLl, 1);
}
}
template<typename TIterator , typename TInteger , int connectivity>
bool DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::retractForward ( ConstIterator &  firstIt,
ConstIterator &  lastIt,
ConstIterator &  nextIt,
Point &  Uf,
Point &  Ul,
Point &  Lf,
Point &  Ll,
const Integer &  s 
)
inlineprivate

Removes the end point of a DSS (pointing to by firstIt)

Parameters:
firstItan iterator pointing to the end of the DSS
lastItan iterator pointing to the other end of the DSS
nextItan iterator pointing to the point of the DSS close to the one pointing to by firstIt
Uffirst upper leaning point
Ullast upper leaning point
Lffirst lower leaning point
Lllast lower leaning point
sa signed integer equal to 1 or -1
Returns:
'true'.

Definition at line 394 of file ArithmeticalDSS.ih.

{
Vector v = Point(*myL)-Point(*myF);
if (Tools<Integer,connectivity>
::norm(v[0],v[1]) <= NumberTraits<Integer>::ONE) {//if there are only two points
//init with nextIt
firstIt = nextIt;
Uf = *firstIt;
Lf = *firstIt;
myA = 0;
myB = 0;
myMu = 0;
myOmega = 0;
myNbUpPat = 0;
myNbLowPat = 0;
mySteps.clear();
} else { //there are strictly more than two points
//update myF
Point ptToRemove = *firstIt;
firstIt = nextIt;
//if the point to remove is the first upper leaning point...
if (ptToRemove == Uf) {
//... and if the first and last lower leaning points are confounded
if (Lf == Ll) {
//update of the parameters:
//a,b
Vector newMainVector = ( Lf - ( Uf + vectorFrom0ToOmega() ) )*s;
myA = newMainVector[1];
myB = newMainVector[0];
//leaning points
Integer k; //repetitions of the newMainVector
Vector toUl = (Ul - Point(*firstIt))*s;
k = Tools<Integer,connectivity>::norm(toUl[0],toUl[1])
/Tools<Integer,connectivity>::norm(myA,myB);
Uf = Ul - newMainVector*k*s;
myNbUpPat = k;
Vector toLastIt = Point(*lastIt) - Lf;
k = Tools<Integer,connectivity>::norm(toLastIt[0],toLastIt[1])
/Tools<Integer,connectivity>::norm(myA,myB);
Ll = Lf + newMainVector*k*s;
myNbLowPat = k;
//mu, omega
myMu = getRemainder(myUl);
myOmega = Tools<Integer,connectivity>::norm(myA,myB);
} else {
Uf = Uf + Vector(myB,myA)*s;
myNbUpPat--;
}
}
//if the point to remove is the first lower leaning point...
if (ptToRemove == Lf) {
//... and if the first and last upper leaning points are confounded
if (Uf == Ul) {
//update of the parameters:
//a,b
Vector newMainVector = ( Uf - (Lf - vectorFrom0ToOmega() ) )*s;
myA = newMainVector[1];
myB = newMainVector[0];
//leaning points
Integer k; //repetitions of the newMainVector
Vector toLl = Ll - Point(*firstIt);
k = Tools<Integer,connectivity>::norm(toLl[0],toLl[1])
/Tools<Integer,connectivity>::norm(myA,myB);
Lf = Ll - newMainVector*k*s;
myNbLowPat = k;
Vector toLastIt = Point(*lastIt) - Uf;
k = Tools<Integer,connectivity>::norm(toLastIt[0],toLastIt[1])
/Tools<Integer,connectivity>::norm(myA,myB);
Ul = Uf + newMainVector*k*s;
myNbUpPat = k;
//mu, omega
myMu = getRemainder(myUl);
myOmega = Tools<Integer,connectivity>::norm(myA,myB);
} else {
Lf = Lf + Vector(myB,myA)*s;
myNbLowPat--;
}
}
//steps update
if (Vector(myB,myA) == mySteps.at(0)) {
Vector tmp(mySteps.at(0));
mySteps.clear();
mySteps.push_back(tmp);
} else if (Vector(myB,myA) == mySteps.at(1)) {
Vector tmp(mySteps.at(1));
mySteps.clear();
mySteps.push_back(tmp);
}
}
return true;
}
template<typename TIterator , typename TInteger , int connectivity>
void DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::selfDisplay ( std::ostream &  out)
inline

Writes/Displays the object on an output stream.

Parameters:
outthe output stream where the object is written.

Definition at line 1015 of file ArithmeticalDSS.ih.

{
out << "[ArithmeticalDSS]" << endl;
out << "Parameters (a,b,mu,omega)=";
out << "("<< myA << ", " << myB << ", ";
out << myMu << ", " << myOmega << ")" << endl;
out << "Number of upper patterns: " << myNbUpPat << endl;
out << "Number of lower patterns: " << myNbLowPat << endl;
out << "First point " << Point(*myF) << " Last point " << Point(*myL) << endl;
out << "Leaning points:" << endl;
out << " Uf " << myUf << endl << " Ul " << myUl << endl;
out << " Lf " << myLf << endl << " Ll " << myLl << endl;
out << "Steps:" << endl;
for (unsigned int i = 0; i < mySteps.size(); i++) {
out << " " << mySteps.at(i) << endl;
}
out << "[End ArithmeticalDSS]" << endl;
}
template<typename TIterator , typename TInteger , int connectivity>
DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::Vector DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::vectorFrom0ToOmega ( ) const
inlineprivate

Returns the 2D vector starting at a point of remainder 0 and pointing to the closer point of remainder omega

Returns:
the 2D vector.

Definition at line 1055 of file ArithmeticalDSS.ih.

{
Vector v = mySteps.at(1) - mySteps.at(0);
if ( getRemainder(v) == myOmega) {
return v;
} else {
return ( mySteps.at(0) - mySteps.at(1) );
}
}

Field Documentation

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Integer DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myA
protected

y-component of the direction vector

Definition at line 630 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Integer DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myB
protected

x-component of the direction vector

Definition at line 634 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
ConstIterator DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myF

ConstIterator pointing to the back of the DSS

Definition at line 691 of file ArithmeticalDSS.h.

Referenced by DGtal::Display2DFactory::drawAsBoundingBox(), DGtal::Display2DFactory::drawAsDigitalPoints(), DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=(), and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator==().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
ConstIterator DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myL

ConstIterator pointing to the front of the DSS

Definition at line 695 of file ArithmeticalDSS.h.

Referenced by DGtal::Display2DFactory::drawAsBoundingBox(), DGtal::Display2DFactory::drawAsDigitalPoints(), DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=(), and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator==().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myLf

First lower leaning point ( of remainder myMu + myOmega - 1 )

Definition at line 680 of file ArithmeticalDSS.h.

Referenced by DGtal::Display2DFactory::drawAsBoundingBox(), DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=(), and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator==().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myLl

Last lower leaning point ( of remainder myMu + myOmega - 1 )

Definition at line 684 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=(), and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator==().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Integer DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myMu
protected

Intercept

Definition at line 638 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Integer DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myNbLowPat
protected

Number of lower patterns ( myLf = myNbLowPat . ( myB , myA ) + myLl )

Definition at line 652 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Integer DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myNbUpPat
protected

Number of upper patterns ( myUf = myNbUpPat . ( myB , myA ) + myUl )

Definition at line 648 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Integer DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myOmega
protected

Thickness

Definition at line 642 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=(), and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator==().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
std::vector<Vector> DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::mySteps
protected

Steps of the DSS (eg. right and up in the first octant)

Definition at line 658 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myUf

First upper leaning point ( of remainder myMu )

Definition at line 672 of file ArithmeticalDSS.h.

Referenced by DGtal::Display2DFactory::drawAsBoundingBox(), DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=(), and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator==().

template<typename TIterator, typename TInteger = typename IteratorCirculatorTraits<TIterator>::Value::Coordinate, int connectivity = 8>
Point DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::myUl

Last upper leaning point ( of remainder myMu )

Definition at line 676 of file ArithmeticalDSS.h.

Referenced by DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator=(), and DGtal::ArithmeticalDSS< TIterator, TInteger, connectivity >::operator==().

The documentation for this class was generated from the following files:
Generated on Wed Dec 19 2012 19:10:50 for DGtal by   doxygen 1.8.1.1