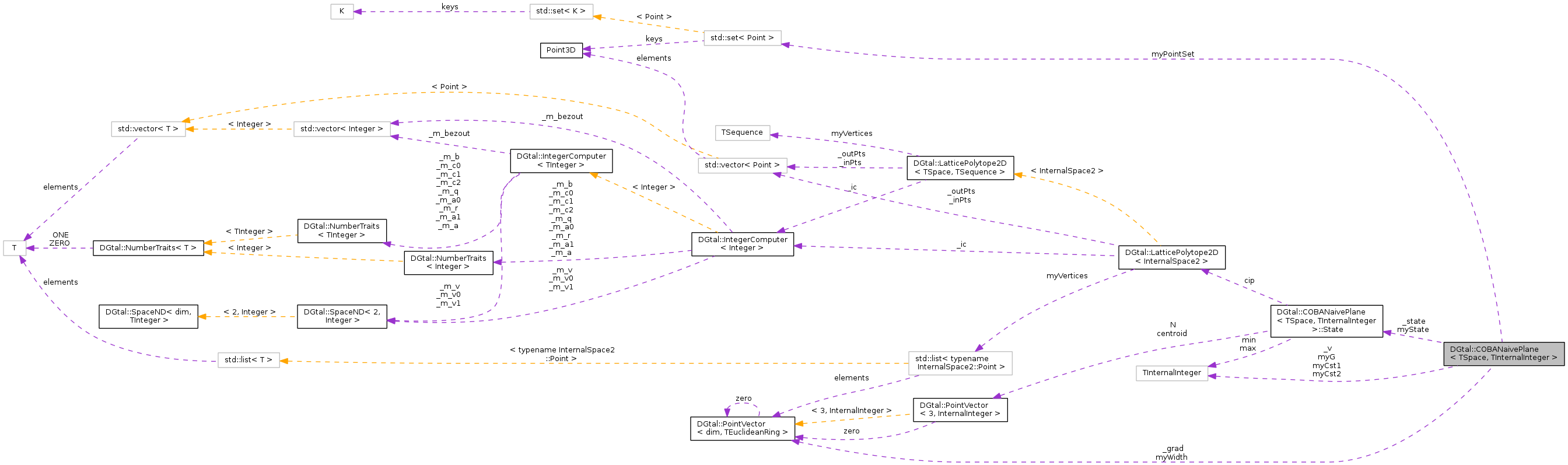
#include <COBANaivePlane.h>

Inheritance diagram for DGtal::COBANaivePlane< TSpace, TInternalInteger >:

Collaboration diagram for DGtal::COBANaivePlane< TSpace, TInternalInteger >:

Data Structures
struct	State

Public Types
typedef TSpace	Space
typedef Space::Point	Point
typedef std::set< Point >	PointSet
typedef PointSet::size_type	Size
typedef PointSet::const_iterator	ConstIterator
typedef PointSet::iterator	Iterator
typedef TInternalInteger	InternalInteger
typedef IntegerComputer < InternalInteger >	MyIntegerComputer
typedef PointSet::const_iterator	const_iterator
typedef PointSet::const_pointer	const_pointer
typedef PointSet::const_reference	const_reference
typedef PointSet::value_type	value_type
typedef PointSet::difference_type	difference_type
typedef PointSet::size_type	size_type

Public Member Functions
	~COBANaivePlane ()
	COBANaivePlane ()
	COBANaivePlane (const COBANaivePlane &other)
COBANaivePlane &	operator= (const COBANaivePlane &other)
MyIntegerComputer &	ic () const
void	clear ()
void	init (Dimension axis, InternalInteger diameter, InternalInteger widthNumerator=NumberTraits< InternalInteger >::ONE, InternalInteger widthDenominator=NumberTraits< InternalInteger >::ONE)
Size	complexity () const
Size	size () const
bool	empty () const
ConstIterator	begin () const
ConstIterator	end () const
Size	max_size () const
Size	maxSize () const
bool	operator() (const Point &p) const
bool	extendAsIs (const Point &p)
bool	extend (const Point &p)
bool	isExtendable (const Point &p) const
template<typename TInputIterator >
bool	extend (TInputIterator it, TInputIterator itE)
template<typename TInputIterator >
bool	isExtendable (TInputIterator it, TInputIterator itE) const
template<typename Vector3D >
void	getNormal (Vector3D &normal) const
template<typename Vector3D >
void	getUnitNormal (Vector3D &normal) const
void	getBounds (double &min, double &max) const
const Point &	minimalPoint () const
const Point &	maximalPoint () const
void	selfDisplay (std::ostream &out) const
bool	isValid () const

Private Types
typedef PointVector < 3, InternalInteger >	InternalPoint3
typedef SpaceND < 2, InternalInteger >	InternalSpace2
typedef InternalSpace2::Point	InternalPoint2
typedef LatticePolytope2D < InternalSpace2 >	ConvexPolygonZ2
typedef ConvexPolygonZ2::HalfSpace	HalfSpace

Private Member Functions
	BOOST_CONCEPT_ASSERT ((CSpace< TSpace >))
	BOOST_CONCEPT_ASSERT ((CInteger< TInternalInteger >))
	BOOST_STATIC_ASSERT ((TSpace::dimension==3))
void	computeCentroidAndNormal (State &state) const
void	doubleCut (InternalPoint2 &grad, State &state) const
template<typename TInputIterator >
void	computeMinMax (State &state, TInputIterator itB, TInputIterator itE) const
template<typename TInputIterator >
bool	updateMinMax (State &state, TInputIterator itB, TInputIterator itE) const
bool	checkPlaneWidth (const State &state) const
void	computeGradient (InternalPoint2 &grad, const State &state) const

Private Attributes
Dimension	myAxis
InternalInteger	myG
InternalPoint2	myWidth
PointSet	myPointSet
State	myState
InternalInteger	myCst1
InternalInteger	myCst2
InternalInteger	_v
State	_state
InternalPoint2	_grad

Detailed Description

template<typename TSpace, typename TInternalInteger>
class DGtal::COBANaivePlane< TSpace, TInternalInteger >

Aim: A class that contains the COBA algorithm (Emilie Charrier, Lilian Buzer, DGCI2008) for recognizing pieces of digital planes of given axis width. When the width is 1, it corresponds to naive planes. The axis is specified at initialization of the object.

Description of template class 'COBANaivePlane'

As a (3D) geometric primitive, it obeys to a subset of the concept CSegmentComputer. It is copy constructible, assignable. It is iterable (inner type ConstIterator, begin(), end()). It has methods extend(), extend( InputIterator, InputIterator) and isExtendable(), isExtendable(InputIterator, InputIterator). The object stores all the distinct points p such that 'extend( p )' was successful. It is thus a model of boost::ForwardContainer (non mutable).

It is also a model of CPointPredicate (returns 'true' iff a point is within the current bounds).

Note on complexity: The complexity is highly dependent on the way points are added to the object. Let D be the diameter and n be the number of points already added. Assume small integers. Complexity of adding a point that do not change the normal of the plane is \( O(\log(n)) \). When it changes the normal, the number of cuts is upper bounded by some \( O(\log(D)) \), each cut costs \( O(n+m\log(D) ) \), where m is the number of sides of the convex polygon of constraints. However, when recognizing a piece of naive plane, the number of times K where the normal should be updated is rather limited to some \( O(\log(D)) \).

Note on execution times: The user should favor int64_t instead of BigInteger whenever possible (diameter smaller than 500). The speed-up is between 10 and 20 for these diameters. For greater diameters, it is necessary to use BigInteger (see below).

Template Parameters:

TSpace	specifies the type of digital space in which lies input digital points. A model of CSpace.
TInternalInteger	specifies the type of integer used in internal computations. The type should be able to hold integers of order (2*D^3)^2 if D is the diameter of the set of digital points. In practice, diameter is limited to 20 for int32_t, diameter is approximately 500 for int64_t, and whatever with BigInteger/GMP integers. For huge diameters, the slow-down is polylogarithmic with the diameter.

Essentially a backport from ImaGene.

   typedef SpaceND<3,int> Z3;
   typedef COBANaivePlane< Z3, int64_t > NaivePlane;
   NaivePlane plane;
   plane.init( 2, 100, 1, 1 ); // axis is z, diameter is 100, width is 1/1 => naive 
   plane.extend( Point( 10, 0, 0 ) ); // return 'true'
   plane.extend( Point( 0, 8, 0 ) );  // return 'true'
   plane.extend( Point( 0, 0, 6 ) );  // return 'true'
   plane.extend( Point( 5, 5, 5 ) );  // return 'false'
   // There is no naive plane going through the 3 first points and the last one.

Model of boost::DefaultConstructible, boost::CopyConstructible, boost::Assignable, boost::ForwardContainer, CPointPredicate.

Definition at line 128 of file COBANaivePlane.h.

Member Typedef Documentation

template<typename TSpace, typename TInternalInteger>

typedef PointSet::const_iterator DGtal::COBANaivePlane< TSpace, TInternalInteger >::const_iterator

Definition at line 148 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::const_pointer DGtal::COBANaivePlane< TSpace, TInternalInteger >::const_pointer

Definition at line 149 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::const_reference DGtal::COBANaivePlane< TSpace, TInternalInteger >::const_reference

Definition at line 150 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::const_iterator DGtal::COBANaivePlane< TSpace, TInternalInteger >::ConstIterator

Definition at line 141 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef LatticePolytope2D< InternalSpace2 > DGtal::COBANaivePlane< TSpace, TInternalInteger >::ConvexPolygonZ2

private

Definition at line 160 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::difference_type DGtal::COBANaivePlane< TSpace, TInternalInteger >::difference_type

Definition at line 152 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef ConvexPolygonZ2::HalfSpace DGtal::COBANaivePlane< TSpace, TInternalInteger >::HalfSpace

private

Definition at line 161 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef TInternalInteger DGtal::COBANaivePlane< TSpace, TInternalInteger >::InternalInteger

Definition at line 143 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef InternalSpace2::Point DGtal::COBANaivePlane< TSpace, TInternalInteger >::InternalPoint2

private

Definition at line 159 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointVector< 3, InternalInteger > DGtal::COBANaivePlane< TSpace, TInternalInteger >::InternalPoint3

private

Definition at line 157 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef SpaceND< 2, InternalInteger > DGtal::COBANaivePlane< TSpace, TInternalInteger >::InternalSpace2

private

Definition at line 158 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::iterator DGtal::COBANaivePlane< TSpace, TInternalInteger >::Iterator

Definition at line 142 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef IntegerComputer< InternalInteger > DGtal::COBANaivePlane< TSpace, TInternalInteger >::MyIntegerComputer

Definition at line 144 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef Space::Point DGtal::COBANaivePlane< TSpace, TInternalInteger >::Point

Definition at line 138 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef std::set< Point > DGtal::COBANaivePlane< TSpace, TInternalInteger >::PointSet

Definition at line 139 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::size_type DGtal::COBANaivePlane< TSpace, TInternalInteger >::Size

Definition at line 140 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::size_type DGtal::COBANaivePlane< TSpace, TInternalInteger >::size_type

Definition at line 153 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef TSpace DGtal::COBANaivePlane< TSpace, TInternalInteger >::Space

Definition at line 137 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

typedef PointSet::value_type DGtal::COBANaivePlane< TSpace, TInternalInteger >::value_type

Definition at line 151 of file COBANaivePlane.h.

Constructor & Destructor Documentation

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::~COBANaivePlane ( )

inline

Destructor.

Definition at line 45 of file COBANaivePlane.ih.

{ // Nothing to do.

}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::COBANaivePlane ( )

inline

Constructor. The object is not valid and should be initialized.

See also:: init

Definition at line 52 of file COBANaivePlane.ih.

  : myG( NumberTraits<TInternalInteger>::ZERO )
{ // Object is invalid
}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::COBANaivePlane ( const COBANaivePlane< TSpace, TInternalInteger > & other )

inline

Copy constructor.

Parameters:

other the object to clone.

Definition at line 60 of file COBANaivePlane.ih.

  : myAxis( other.myAxis ),
    myG( other.myG ),
    myWidth( other.myWidth ),
    myPointSet( other.myPointSet ),
    myState( other.myState ),
    myCst1( other.myCst1 ),
    myCst2( other.myCst2 )
{
}

Member Function Documentation

template<typename TSpace, typename TInternalInteger>

ConstIterator DGtal::COBANaivePlane< TSpace, TInternalInteger >::begin ( ) const

Returns:: a const iterator pointing on the first point stored in the current naive plane.

template<typename TSpace, typename TInternalInteger>

DGtal::COBANaivePlane< TSpace, TInternalInteger >::BOOST_CONCEPT_ASSERT ( (CSpace< TSpace >) )

private

template<typename TSpace, typename TInternalInteger>

DGtal::COBANaivePlane< TSpace, TInternalInteger >::BOOST_CONCEPT_ASSERT ( (CInteger< TInternalInteger >) )

private

template<typename TSpace, typename TInternalInteger>

DGtal::COBANaivePlane< TSpace, TInternalInteger >::BOOST_STATIC_ASSERT ( (TSpace::dimension==3) )

private

template<typename TSpace , typename TInternalInteger >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::checkPlaneWidth ( const State & state ) const

private

Parameters:

state the state where the normal state.N, the scalars state.min and state.max are used in computations.

Returns:: 'true' if the current width along state.N (computed from the difference of state.max and state.min) is strictly inferior to the maximal specified width (in myWidth), 'false' otherwise.

Definition at line 771 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::max, DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::min, and DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::N.

{
  _v = ic().abs( state.N[ myAxis ] );
  return ( ( state.max - state.min ) 
           < ( _v * myWidth[ 0 ] / myWidth[ 1 ] ) );
}

template<typename TSpace , typename TInternalInteger >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::clear ( )

inline

Clear the object, free memory. The plane keeps its main axis, diameter and width, but contains no point.

Definition at line 103 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::clear().

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::clear().

{
  myPointSet.clear();
  myState.cip.clear();
  // initialize the search space as a square.
  myState.cip.pushBack( InternalPoint2( -myG, -myG ) ); 
  myState.cip.pushBack( InternalPoint2(  myG, -myG ) ); 
  myState.cip.pushBack( InternalPoint2(  myG,  myG ) ); 
  myState.cip.pushBack( InternalPoint2( -myG,  myG ) ); 
  computeCentroidAndNormal( myState );
}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::Size DGtal::COBANaivePlane< TSpace, TInternalInteger >::complexity ( ) const

inline

Returns:: the number of vertices/edges of the convex integer polygon of solutions.

Definition at line 176 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::size().

{
  return myState.cip.size();
}

template<typename TSpace , typename TInternalInteger >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::computeCentroidAndNormal ( State & state ) const

inlineprivate

Recompute centroid of polygon of solution and deduce the current normal vector. It is called after any modification of the convex polygon representing the set of solution.

Parameters:

state (modified) the state where the fields state.cip are used in computation and where fields state.centroid and state.N are updated.

Definition at line 665 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::centroid, DGtal::LatticePolytope2D< TSpace, TSequence >::centroid(), DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::cip, DGtal::LatticePolytope2D< TSpace, TSequence >::empty(), and DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::N.

{
  if ( state.cip.empty() ) return;
  state.centroid = state.cip.centroid();
  ic().reduce( state.centroid );
  switch( myAxis ){
  case 0 : 
    state.N[ 0 ] = state.centroid[ 2 ] * myG;
    state.N[ 1 ] = state.centroid[ 0 ];
    state.N[ 2 ] = state.centroid[ 1 ];
    break;
  case 1 : 
    state.N[ 0 ] = state.centroid[ 0 ];
    state.N[ 1 ] = state.centroid[ 2 ] * myG;
    state.N[ 2 ] = state.centroid[ 1 ];
    break;
  case 2 : 
    state.N[ 0 ] = state.centroid[ 0 ];
    state.N[ 1 ] = state.centroid[ 1 ];
    state.N[ 2 ] = state.centroid[ 2 ] * myG;
    break;
  }
}

template<typename TSpace , typename TInternalInteger >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::computeGradient	(	InternalPoint2 &	grad,
		const State &	state
	)		const

private

Parameters:

grad	(updated) the value of a gradient used to cut the polygon of solutions.
state	the state where the iterators state.indMin and state.indMax are used in computations.

Definition at line 781 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMax, and DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMin.

{
  // computation of the gradient
  switch( myAxis ){
  case 0 : 
    grad[ 0 ] = state.ptMin[ 1 ] - state.ptMax[ 1 ];
    grad[ 1 ] = state.ptMin[ 2 ] - state.ptMax[ 2 ];
    break;
  case 1:
    grad[ 0 ] = state.ptMin[ 0 ] - state.ptMax[ 0 ];
    grad[ 1 ] = state.ptMin[ 2 ] - state.ptMax[ 2 ];
    break;
  case 2:
    grad[ 0 ] = state.ptMin[ 0 ] - state.ptMax[ 0 ];
    grad[ 1 ] = state.ptMin[ 1 ] - state.ptMax[ 1 ];
    break;
  }
}

template<typename TSpace , typename TInternalInteger >

template<typename TInputIterator >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::computeMinMax	(	State &	state,
		TInputIterator	itB,
		TInputIterator	itE
	)		const

private

Computes the min and max values/arguments of the scalar product between the normal state.N and the points in the range [itB,itE). Overwrites state.min, state.max at the start.

Template Parameters:

TInputIterator any model of InputIterator.

Parameters:

state	(modified) the state where the normal N is used in computation and where fields state.min, state.max, state.indMin, state.indMax are updated.
itB	an input iterator on the first point of the range.
itE	an input iterator after the last point of the range.

Definition at line 712 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::max, DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::min, DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::N, DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMax, and DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMin.

{
  BOOST_CONCEPT_ASSERT(( boost::InputIterator<TInputIterator> ));
  ASSERT( itB != itE );
  ic().getDotProduct( state.min, state.N, *itB );
  state.max = state.min;
  state.ptMax = state.ptMin = *itB;
  ++itB;
  // look for the points defining the min dot product and the max dot product
  for ( ; itB != itE; ++itB )
    {
      ic().getDotProduct( _v, state.N, *itB );
      if ( _v > state.max ) 
        { 
          state.max = _v;  
          state.ptMax = *itB;
        }
      else if ( _v < state.min )
        {
          state.min = _v;
          state.ptMin = *itB;
        }
    }
}

template<typename TSpace , typename TInternalInteger >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::doubleCut	(	InternalPoint2 &	grad,
		State &	state
	)		const

inlineprivate

Performs the double cut in parameter space according to the current gradient and width. The centroid and normals are no more valid (computeCentroidAndNormal should be called afterwards).

Parameters:

grad	(altered, but not modified) the gradient used to update the polygon of solutions state.cip.
state	(modified) the state where the fields state.indMin, state.indMax, state.cip are used in computation and where field state.cip is updated.

Definition at line 694 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::cip, DGtal::LatticePolytope2D< TSpace, TSequence >::cut(), DGtal::PointVector< dim, TEuclideanRing >::negate(), DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMax, and DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMin.

{
  // 2 cuts on the search space:
  //  Gradient.p <= cst1 - _v
  // -Gradient.p <= cst2 + _v
  _v = myG * ( state.ptMin[ myAxis ] 
               - state.ptMax[ myAxis ] );
  state.cip.cut( HalfSpace( grad, myCst1 - _v ) );
  grad.negate();
  state.cip.cut( HalfSpace( grad, myCst2 + _v ) );
  grad.negate();
}

template<typename TSpace , typename TInternalInteger >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::empty ( ) const

inline

Returns:: 'true' if and only if this object contains no point.

Definition at line 149 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::empty().

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::empty().

{
  return myPointSet.empty();
}

template<typename TSpace, typename TInternalInteger>

ConstIterator DGtal::COBANaivePlane< TSpace, TInternalInteger >::end ( ) const

Returns:: a const iterator pointing after the last point stored in the current naive plane.

template<typename TSpace , typename TInternalInteger >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::extend ( const Point & p )

Adds the point p and checks if we have still a digital plane of specified width. The plane parameters may be updated so as to include the new point.

Parameters:

p	any 3D point (in the specified diameter).

Returns:: 'true' if it is still a plane, 'false' otherwise (the object is then in its original state).

Definition at line 207 of file COBANaivePlane.ih.

{
  ASSERT( isValid() );
  // Checks if first point.
  if ( empty() )
    {
      myPointSet.insert( p );
      ic().getDotProduct( myState.max, myState.N, p );
      myState.min = myState.max;
      myState.ptMax = myState.ptMin = p;
      return true;
    }
  // Check first if p is already a point of the plane.
  if ( myPointSet.find( p ) != myPointSet.end() ) // already in set
    return true;
  // Check if p lies within the current bounds of the plane.
  _state.N = myState.N; 
  _state.min = myState.min; 
  _state.max = myState.max; 
  _state.ptMin = myState.ptMin; 
  _state.ptMax = myState.ptMax; 
  bool changed = updateMinMax( _state, &p, (&p)+1 );
  // Check if point is already within bounds.
  if ( ! changed ) 
    {
      myPointSet.insert( p );
      return true;
    }
  // Check if width is still ok
  if ( checkPlaneWidth( _state ) )
    {
      myState.min = _state.min;
      myState.max = _state.max;
      myState.ptMin = _state.ptMin;
      myState.ptMax = _state.ptMax;
      myPointSet.insert( p );
      return true;
    }
  // We have to find a new normal. First, update gradient.
  computeGradient( _grad, _state );
  // Checks if we can change the normal so as to find another digital plane.
  if( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
        && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
    {
      // Unable to update solution. 
      return false;
    }
  // There is a gradient, tries to optimize.
  _state.cip = myState.cip;
  doubleCut( _grad, _state );
  // While at least 1 point left on the search space
  while ( ! _state.cip.empty() )
  {
    computeCentroidAndNormal( _state );
    // Calls oracle
    computeMinMax( _state, myPointSet.begin(), myPointSet.end() );
    updateMinMax( _state, &p, (&p)+1 );
    // Check if width is now ok
    if ( checkPlaneWidth( _state ) )
      { // Found a plane.
        myState.min = _state.min;
        myState.max = _state.max;
        myState.ptMin = _state.ptMin;
        myState.ptMax = _state.ptMax;
        myState.cip.swap( _state.cip );
        myState.centroid = _state.centroid;
        myState.N = _state.N;
        myPointSet.insert( p );
        return true;
      }
    // We have to find a new normal. First, update gradient.
    computeGradient( _grad, _state );
    // Checks if we can change the normal so as to find another digital plane.
    if ( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
           && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
      {
        // Unable to update solution. Removes point from set.
        break;
      }
    // There is a gradient, tries to optimize.
    doubleCut( _grad, _state );
  }
  // was unable to find a correct plane.
  return false;
}

template<typename TSpace , typename TInternalInteger >

template<typename TInputIterator >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::extend	(	TInputIterator	it,
		TInputIterator	itE
	)

Adds the range of points [it, itE) and checks if we have still a digital plane of specified width. The plane parameters may be updated so as to include all the new points. All points pointed by iterators should be in the diameter of this object.

Template Parameters:

TInputIterator any model of InputIterator on Point.

Parameters:

it	an iterator on the first element of the range of 3D points.
itE	an iterator after the last element of the range of 3D points.

Returns:: 'true' if it is still a plane, 'false' otherwise (the object is then in its original state).

Definition at line 369 of file COBANaivePlane.ih.

{
  BOOST_CONCEPT_ASSERT(( boost::InputIterator<TInputIterator> ));
  ASSERT( isValid() );
  // Check if points lies within the current bounds of the plane.
  bool changed;
  _state.N = myState.N; 
  if ( empty() )
    {
      changed = true;
      computeMinMax( _state, it, itE );
    }
  else
    {
      _state.min = myState.min; 
      _state.max = myState.max; 
      _state.ptMin = myState.ptMin; 
      _state.ptMax = myState.ptMax; 
      changed = updateMinMax( _state, it, itE );
    }
  // Check if points are already within bounds.
  if ( ! changed ) 
    { // All points are within bounds. Put them in pointset.
      for ( TInputIterator tmpIt = it; tmpIt != itE; ++tmpIt )
        myPointSet.insert( *tmpIt );
      return true;
    }
  // Check if width is still ok
  if ( checkPlaneWidth( _state ) )
    {
      myState.min = _state.min;
      myState.max = _state.max;
      myState.ptMin = _state.ptMin;
      myState.ptMax = _state.ptMax;
      for ( TInputIterator tmpIt = it; tmpIt != itE; ++tmpIt )
        myPointSet.insert( *tmpIt );
      return true;
    }
  // We have to find a new normal. First, update gradient.
  computeGradient( _grad, _state );
  // Checks if we can change the normal so as to find another digital plane.
  if( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
        && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
    {
      // Unable to update solution. 
      return false;
    }
  // There is a gradient, tries to optimize.
  _state.cip = myState.cip;
  doubleCut( _grad, _state );
  // While at least 1 point left on the search space
  while ( ! _state.cip.empty() )
  {
    computeCentroidAndNormal( _state );
    // Calls oracle
    computeMinMax( _state, myPointSet.begin(), myPointSet.end() );
    updateMinMax( _state, it, itE );
    // Check if width is now ok
    if ( checkPlaneWidth( _state ) )
      { // Found a plane.
        myState.min = _state.min;
        myState.max = _state.max;
        myState.ptMin = _state.ptMin;
        myState.ptMax = _state.ptMax;
        myState.cip.swap( _state.cip );
        myState.centroid = _state.centroid;
        myState.N = _state.N;
        for ( TInputIterator tmpIt = it; tmpIt != itE; ++tmpIt )
          myPointSet.insert( *tmpIt );
        return true;
      }
    // We have to find a new normal. First, update gradient.
    computeGradient( _grad, _state );
    // Checks if we can change the normal so as to find another digital plane.
    if ( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
           && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
      {
        // Unable to update solution. Removes point from set.
        break;
      }
    // There is a gradient, tries to optimize.
    doubleCut( _grad, _state );
  }
  // was unable to find a correct plane.
  return false;
}

template<typename TSpace , typename TInternalInteger >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::extendAsIs ( const Point & p )

inline

Adds the point p to this plane if it is within the current bounds. The plane parameters are not updated.

Parameters:

p	any 3D point (in the specified diameter).

Returns:: 'true' if p is in the plane, 'false' otherwise (the object is then in its original state).

Definition at line 195 of file COBANaivePlane.ih.

{ 
  ASSERT( isValid() && ! empty() );
  bool ok = this->operator()( p );
  if ( ok ) myPointSet.insert( p );
  return ok;
}

template<typename TSpace , typename TInternalInteger >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::getBounds	(	double &	min,
		double &	max
	)		const

inline

If n is the unit normal to the current plane, then n.x >= min and n.x <= max are the two half-planes defining it.

Parameters:

min	the lower bound (corresponding to the unit vector).
max	the upper bound (corresponding to the unit vector).

Definition at line 586 of file COBANaivePlane.ih.

References DGtal::NumberTraits< T >::castToDouble().

{
  double nx = NumberTraits<InternalInteger>::castToDouble( myState.N[ 0 ] );
  double ny = NumberTraits<InternalInteger>::castToDouble( myState.N[ 1 ] );
  double nz = NumberTraits<InternalInteger>::castToDouble( myState.N[ 2 ] );
  double l = sqrt( nx*nx + ny*ny + nz*nz );
  min = NumberTraits<InternalInteger>::castToDouble( myState.min ) / l;
  max = NumberTraits<InternalInteger>::castToDouble( myState.max ) / l;
}

template<typename TSpace , typename TInternalInteger >

template<typename Vector3D >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::getNormal ( Vector3D & normal ) const

inline

Template Parameters:

Vector3D any type T such that T.operator[](int i) returns a reference to a double. i ranges in 0,1,2.

Parameters:

(updates) the current normal vector

Definition at line 544 of file COBANaivePlane.ih.

References DGtal::NumberTraits< T >::castToDouble().

{
  switch( myAxis ) {
    case 0 : 
      normal[0] = 1.0;
      normal[1] = NumberTraits<InternalInteger>::castToDouble( myState.N[ 1 ]) / NumberTraits<InternalInteger>::castToDouble( myState.N[ 0 ] );
      normal[2] = NumberTraits<InternalInteger>::castToDouble( myState.N[ 2 ]) / NumberTraits<InternalInteger>::castToDouble( myState.N[ 0 ] );
      break;
    case 1 : 
      normal[0] = NumberTraits<InternalInteger>::castToDouble( myState.N[ 0 ]) / NumberTraits<InternalInteger>::castToDouble( myState.N[ 1 ] );
      normal[1] = 1.0;
      normal[2] = NumberTraits<InternalInteger>::castToDouble( myState.N[ 2 ]) / NumberTraits<InternalInteger>::castToDouble( myState.N[ 1 ] );
      break;
    case 2 : 
      normal[0] = NumberTraits<InternalInteger>::castToDouble( myState.N[ 0 ]) / NumberTraits<InternalInteger>::castToDouble( myState.N[ 2 ] );
      normal[1] = NumberTraits<InternalInteger>::castToDouble( myState.N[ 1 ]) / NumberTraits<InternalInteger>::castToDouble( myState.N[ 2 ] );
      normal[2] = 1.0;
      break;
  }
}

template<typename TSpace , typename TInternalInteger >

template<typename Vector3D >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::getUnitNormal ( Vector3D & normal ) const

inline

Template Parameters:

Vector3D any type T such that T.operator[](int i) returns a reference to a double. i ranges in 0,1,2.

Parameters:

(updates) the current unit normal vector

Definition at line 571 of file COBANaivePlane.ih.

{
  getNormal( normal );
  double l = sqrt( normal[ 0 ] * normal[ 0 ]
                   + normal[ 1 ] * normal[ 1 ]
                   + normal[ 2 ] * normal[ 2 ] );
  normal[ 0 ] /= l;
  normal[ 1 ] /= l;
  normal[ 2 ] /= l;
}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::MyIntegerComputer & DGtal::COBANaivePlane< TSpace, TInternalInteger >::ic ( ) const

inline

Returns:: the object that performs integer calculation.

Definition at line 94 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::ic().

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::ic().

{
  return myState.cip.ic();
}

template<typename TSpace , typename TInternalInteger >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::init	(	Dimension	axis,
		InternalInteger	diameter,
		InternalInteger	widthNumerator = `NumberTraits< InternalInteger >::ONE`,
		InternalInteger	widthDenominator = `NumberTraits< InternalInteger >::ONE`
	)

inline

All these parameters cannot be changed during the process. After this call, the object is in a consistent state and can accept new points for recognition. Calls clear so that the object is ready to be extended.

Parameters:

axis	the main axis (0,1,2) for x, y or z.
diameter	the diameter for the set of points (maximum distance between the given points)
widthNumerator	the maximal axis-width (x,y,or z) for the plane is defined as the rational number widthNumerator / widthDenominator (default is 1/1, i.e. naive plane).
widthDenominator	the maximal axis-width (x,y,or z) for the plane is defined as the rational number widthNumerator / widthDenominator (default is 1/1, i.e. naive plane).

Definition at line 119 of file COBANaivePlane.ih.

{
  myAxis = axis;
  myWidth[ 0 ] = widthNumerator;
  myWidth[ 1 ] = widthDenominator;
  // initialize the grid step.
  myG = 2*diameter;  myG *= diameter;  myG *= diameter;
  // Initializes some constants
  // _cst1 = ( (int) ceil( get_si( myG ) * myWidth ) + 1 );
  // _cst2 = ( (int) floor( get_si( myG ) * myWidth ) - 1 );
  myCst1 = ( ( myG * myWidth[ 0 ] - 1 ) / myWidth[ 1 ] ) + 2;
  myCst2 = ( ( myG * myWidth[ 0 ] )     / myWidth[ 1 ] ) - 1;
  clear();
}

template<typename TSpace , typename TInternalInteger >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::isExtendable ( const Point & p ) const

Checks if we have still a digital plane of specified width when adding point p. The object is left unchanged whatever the returned value. The invariant is 'this->isExtendable( p ) == true <=> this->extend( p ) == true'.

Parameters:

p	any 3D point (in the specified diameter).

Returns:: 'true' if this is still a plane, 'false' otherwise.

Definition at line 303 of file COBANaivePlane.ih.

{
  ASSERT( isValid() );
  // Checks if first point.
  if ( empty() ) return true;
  // Check first if p is already a point of the plane.
  if ( myPointSet.find( p ) != myPointSet.end() ) // already in set
    return true;
  // Check if p lies within the current bounds of the plane.
  _state.N = myState.N; 
  _state.min = myState.min; 
  _state.max = myState.max; 
  _state.ptMin = myState.ptMin; 
  _state.ptMax = myState.ptMax; 
  bool changed = updateMinMax( _state, (&p), (&p)+1 );
  // Check if point is already within bounds.
  if ( ! changed ) return true;
  // Check if width is still ok
  if ( checkPlaneWidth( _state ) )
    return true;
  // We have to find a new normal. First, update gradient.
  computeGradient( _grad, _state );
  // Checks if we can change the normal so as to find another digital plane.
  if( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
        && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
    // Unable to update solution. 
    return false;
  // There is a gradient, tries to optimize.
  _state.cip = myState.cip;
  doubleCut( _grad, _state );
  // While at least 1 point left on the search space
  while ( ! _state.cip.empty() )
  {
    computeCentroidAndNormal( _state );
    // Calls oracle
    computeMinMax( _state, myPointSet.begin(), myPointSet.end() );
    updateMinMax( _state, (&p), (&p)+1 );
    // Check if width is now ok
    if ( checkPlaneWidth( _state ) )
      // Found a plane.
      return true;
    // We have to find a new normal. First, update gradient.
    computeGradient( _grad, _state );
    // Checks if we can change the normal so as to find another digital plane.
    if ( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
           && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
      // Unable to update solution. 
      return false;
    
    // There is a gradient, tries to optimize.
    doubleCut( _grad, _state );
  }
  // was unable to find a correct plane.
  return false;
}

template<typename TSpace , typename TInternalInteger >

template<typename TInputIterator >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::isExtendable	(	TInputIterator	it,
		TInputIterator	itE
	)		const

Checks if we have still a digital plane of specified width when adding the range of points [it, itE). The object is left unchanged whatever the returned value. All points pointed by iterators should be in the diameter of this object. The invariant is 'this->isExtendable( it, itE ) == true <=> this->extend( it, itE ) == true'.

Template Parameters:

TInputIterator any model of InputIterator on Point.

Parameters:

it	an iterator on the first element of the range of 3D points.
itE	an iterator after the last element of the range of 3D points.

Returns:: 'true' if this is still a plane, 'false' otherwise.

Definition at line 468 of file COBANaivePlane.ih.

{
  BOOST_CONCEPT_ASSERT(( boost::InputIterator<TInputIterator> ));
  ASSERT( isValid() );
  // Check if points lies within the current bounds of the plane.
  bool changed;
  _state.N = myState.N; 
  if ( empty() )
    {
      changed = true;
      computeMinMax( _state, it, itE );
    }
  else
    {
      _state.N = myState.N; 
      _state.min = myState.min; 
      _state.max = myState.max; 
      _state.ptMin = myState.ptMin; 
      _state.ptMax = myState.ptMax; 
      changed = updateMinMax( _state, it, itE );
    }
  // Check if point is already within bounds.
  if ( ! changed ) return true;
  // Check if width is still ok
  if ( checkPlaneWidth( _state ) )
    return true;
  // We have to find a new normal. First, update gradient.
  computeGradient( _grad, _state );
  // Checks if we can change the normal so as to find another digital plane.
  if( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
        && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
    // Unable to update solution. 
    return false;
  // There is a gradient, tries to optimize.
  _state.cip = myState.cip;
  doubleCut( _grad, _state );
  // While at least 1 point left on the search space
  while ( ! _state.cip.empty() )
  {
    computeCentroidAndNormal( _state );
    // Calls oracle
    computeMinMax( _state, myPointSet.begin(), myPointSet.end() );
    updateMinMax( _state, it, itE );
    // Check if width is now ok
    if ( checkPlaneWidth( _state ) )
      // Found a plane.
      return true;
    // We have to find a new normal. First, update gradient.
    computeGradient( _grad, _state );
    // Checks if we can change the normal so as to find another digital plane.
    if ( ( ( _grad[ 0 ] == NumberTraits<InternalInteger>::ZERO )
           && ( _grad[ 1 ] == NumberTraits<InternalInteger>::ZERO ) ) )
      // Unable to update solution. 
      return false;
    
    // There is a gradient, tries to optimize.
    doubleCut( _grad, _state );
  }
  // was unable to find a correct plane.
  return false;
}

template<typename TSpace , typename TInternalInteger >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::isValid ( ) const

inline

Checks the validity/consistency of the object.

Returns:: 'true' if the object is valid, 'false' otherwise.

Definition at line 651 of file COBANaivePlane.ih.

{
  return myG != NumberTraits< InternalInteger >::ZERO;
}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::Size DGtal::COBANaivePlane< TSpace, TInternalInteger >::max_size ( ) const

inline

NB: std version.

Returns:: the maximal allowed number of points in the current naive plane.

See also:: maxSize

Definition at line 158 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::max_size().

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::max_size().

{
  return myPointSet.max_size();
}

template<typename TSpace , typename TInternalInteger >

const DGtal::COBANaivePlane< TSpace, TInternalInteger >::Point & DGtal::COBANaivePlane< TSpace, TInternalInteger >::maximalPoint ( ) const

inline

Precondition:: ! empty()

Returns:: the current maximal point of the plane, i.e. the one with the highest scalar product with the current normal vector. Note that other points may also have a maximum value.

Definition at line 610 of file COBANaivePlane.ih.

{
  ASSERT( ! this->empty() );
  return *(myState.indMax);
}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::Size DGtal::COBANaivePlane< TSpace, TInternalInteger >::maxSize ( ) const

inline

same as max_size

Returns:: the maximal allowed number of points in the current naive plane.

Definition at line 167 of file COBANaivePlane.ih.

{
  return max_size();
}

template<typename TSpace , typename TInternalInteger >

const DGtal::COBANaivePlane< TSpace, TInternalInteger >::Point & DGtal::COBANaivePlane< TSpace, TInternalInteger >::minimalPoint ( ) const

inline

Precondition:: ! empty()

Returns:: the current minimal point of the plane, i.e. the one with the smallest scalar product with the current normal vector. Note that other points may also have a minimum value.

Definition at line 600 of file COBANaivePlane.ih.

{
  ASSERT( ! this->empty() );
  return *(myState.indMin);
}

template<typename TSpace , typename TInternalInteger >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator() ( const Point & p ) const

inline

Checks if the point p is in the current digital plane. Therefore, a COBANaivePlane is a model of CPointPredicate.

Parameters:

p	any 3D point.

Returns:: 'true' if it is in the current plane, false otherwise.

Definition at line 185 of file COBANaivePlane.ih.

{
  ic().getDotProduct( _v, myState.N, p );
  return ( _v >= myState.min ) && ( _v <= myState.max );
}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger > & DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator= ( const COBANaivePlane< TSpace, TInternalInteger > & other )

inline

Assignment.

Parameters:

other the object to copy.

Returns:: a reference on 'this'.

Definition at line 75 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::myAxis, DGtal::COBANaivePlane< TSpace, TInternalInteger >::myCst1, DGtal::COBANaivePlane< TSpace, TInternalInteger >::myCst2, DGtal::COBANaivePlane< TSpace, TInternalInteger >::myG, DGtal::COBANaivePlane< TSpace, TInternalInteger >::myPointSet, DGtal::COBANaivePlane< TSpace, TInternalInteger >::myState, and DGtal::COBANaivePlane< TSpace, TInternalInteger >::myWidth.

{
  if ( this != &other )
    {
      myAxis = other.myAxis;
      myG = other.myG;
      myWidth = other.myWidth;
      myPointSet = other.myPointSet;
      myState = other.myState;
      myCst1 = other.myCst1;
      myCst2 = other.myCst2;
    }
  return *this;
}

template<typename TSpace , typename TInternalInteger >

void DGtal::COBANaivePlane< TSpace, TInternalInteger >::selfDisplay ( std::ostream & out ) const

inline

Writes/Displays the object on an output stream.

Parameters:

out	the output stream where the object is written.

Definition at line 628 of file COBANaivePlane.ih.

{
  double min, max;
  double N[ 3 ];
  out << "[COBANaivePlane"
      << " axis=" << myAxis << " w=" << myWidth[ 0 ] << "/" << myWidth[ 1 ]
      << " size=" << size() << " complexity=" << complexity() << " N=" << myState.N << ": ";
  this->getUnitNormal( N );
  this->getBounds( min, max );
  out << min << " <= " 
      << N[ 0 ] << " * x + "
      << N[ 1 ] << " * y + "
      << N[ 2 ] << " * z "
      << " <= " << max << " ]"; 
}

template<typename TSpace , typename TInternalInteger >

DGtal::COBANaivePlane< TSpace, TInternalInteger >::Size DGtal::COBANaivePlane< TSpace, TInternalInteger >::size ( ) const

inline

Returns:: the number of distinct points in the current naive plane.

Definition at line 140 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::size().

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::complexity(), and DGtal::COBANaivePlane< TSpace, TInternalInteger >::size().

{
  return myPointSet.size();
}

template<typename TSpace , typename TInternalInteger >

template<typename TInputIterator >

bool DGtal::COBANaivePlane< TSpace, TInternalInteger >::updateMinMax	(	State &	state,
		TInputIterator	itB,
		TInputIterator	itE
	)		const

private

Updates the min and max values/arguments of the scalar product between the normal state.N and the points in the range [itB,itE). Do not overwrite state.min, state.max at the start.

Template Parameters:

TInputIterator any model of InputIterator.

Parameters:

state	(modified) the state where the normal N is used in computation and where fields state.min, state.max, state.indMin, state.indMax are updated.
itB	an input iterator on the first point of the range.
itE	an input iterator after the last point of the range.

Returns:: 'true' if any of the fields state.min, state.max, state.indMin, state.indMax have been updated, 'false' otherwise.

Definition at line 742 of file COBANaivePlane.ih.

References DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::max, DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::min, DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::N, DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMax, and DGtal::COBANaivePlane< TSpace, TInternalInteger >::State::ptMin.

{
  BOOST_CONCEPT_ASSERT(( boost::InputIterator<TInputIterator> ));
  bool changed = false;
  // look for the points defining the min dot product and the max dot product
  for ( ; itB != itE; ++itB )
    {
      ic().getDotProduct( _v, state.N, *itB );
      if ( _v > state.max ) 
        { 
          state.max = _v;  
          state.ptMax = *itB;
          changed = true;
        }
      else if ( _v < state.min )
        {
          state.min = _v;
          state.ptMin = *itB;
          changed = true;
        }
    }
  return changed;
}

Field Documentation

template<typename TSpace, typename TInternalInteger>

InternalPoint2 DGtal::COBANaivePlane< TSpace, TInternalInteger >::_grad

mutableprivate

temporary variable to store the current gradient.

Definition at line 441 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

State DGtal::COBANaivePlane< TSpace, TInternalInteger >::_state

mutableprivate

Temporary state used in computations.

Definition at line 440 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

InternalInteger DGtal::COBANaivePlane< TSpace, TInternalInteger >::_v

mutableprivate

temporary variable used in computations.

Definition at line 439 of file COBANaivePlane.h.

template<typename TSpace, typename TInternalInteger>

Dimension DGtal::COBANaivePlane< TSpace, TInternalInteger >::myAxis

private

the main axis used in all subsequent computations.

Definition at line 432 of file COBANaivePlane.h.

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator=().

template<typename TSpace, typename TInternalInteger>

InternalInteger DGtal::COBANaivePlane< TSpace, TInternalInteger >::myCst1

private

( (int) ceil( get_si( myG ) * myWidth ) + 1 ).

Definition at line 437 of file COBANaivePlane.h.

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator=().

template<typename TSpace, typename TInternalInteger>

InternalInteger DGtal::COBANaivePlane< TSpace, TInternalInteger >::myCst2

private

( (int) floor( get_si( myG ) * myWidth ) - 1 ).

Definition at line 438 of file COBANaivePlane.h.

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator=().

template<typename TSpace, typename TInternalInteger>

InternalInteger DGtal::COBANaivePlane< TSpace, TInternalInteger >::myG

private

the grid step used in all subsequent computations.

Definition at line 433 of file COBANaivePlane.h.

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator=().

template<typename TSpace, typename TInternalInteger>

PointSet DGtal::COBANaivePlane< TSpace, TInternalInteger >::myPointSet

private

the set of points within the plane.

Definition at line 435 of file COBANaivePlane.h.

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator=().

template<typename TSpace, typename TInternalInteger>

State DGtal::COBANaivePlane< TSpace, TInternalInteger >::myState

private

the current state that defines the plane being recognized.

Definition at line 436 of file COBANaivePlane.h.

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator=().

template<typename TSpace, typename TInternalInteger>

InternalPoint2 DGtal::COBANaivePlane< TSpace, TInternalInteger >::myWidth

private

the plane width as a positive rational number myWidth[0]/myWidth[1]

Definition at line 434 of file COBANaivePlane.h.

Referenced by DGtal::COBANaivePlane< TSpace, TInternalInteger >::operator=().

The documentation for this class was generated from the following files:

Data Structures

Public Types

Public Member Functions

Private Types

Private Member Functions

Private Attributes

Detailed Description

template<typename TSpace, typename TInternalInteger> class DGtal::COBANaivePlane< TSpace, TInternalInteger >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Field Documentation

template<typename TSpace, typename TInternalInteger>
class DGtal::COBANaivePlane< TSpace, TInternalInteger >