#include <GaussDigitizer.h>

Collaboration diagram for DGtal::GaussDigitizer< TSpace, TEuclideanShape >:

Public Types
typedef TSpace	Space
typedef Space::Integer	Integer
typedef Space::Point	Point
typedef Space::Vector	Vector
typedef Space::RealPoint	RealPoint
typedef Space::RealPoint	RealVector
typedef TEuclideanShape	EuclideanShape
typedef HyperRectDomain< Space >	Domain
typedef RegularPointEmbedder < Space >	PointEmbedder

Public Member Functions
	BOOST_CONCEPT_ASSERT ((CEuclideanOrientedShape< TEuclideanShape >))
	~GaussDigitizer ()
	GaussDigitizer ()
GaussDigitizer &	operator= (const GaussDigitizer &other)
void	attach (const EuclideanShape &shape)
void	init (const RealPoint &xLow, const RealPoint &xUp, typename RealVector::Component gridStep)
void	init (const RealPoint &xLow, const RealPoint &xUp, const RealVector &gridSteps)
const PointEmbedder &	pointEmbedder () const
Domain	getDomain () const
Point	floor (const RealPoint &p) const
Point	ceil (const RealPoint &p) const
Point	round (const RealPoint &p) const
RealPoint	embed (const Point &p) const
Orientation	orientation (const Point &p) const
bool	operator() (const Point &p) const
const Point &	getLowerBound () const
const Point &	getUpperBound () const
Vector	resolution () const
RealVector	gridSteps () const
void	selfDisplay (std::ostream &out) const
bool	isValid () const

Protected Attributes
const EuclideanShape *	myEShape
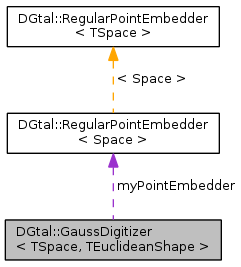
RegularPointEmbedder< Space >	myPointEmbedder
Point	myLowerPoint
Point	myUpperPoint

Detailed Description

template<typename TSpace, typename TEuclideanShape>
class DGtal::GaussDigitizer< TSpace, TEuclideanShape >

Aim: A class for computing the Gauss digitization of some Euclidean shape, i.e. its intersection with some \( h_1 Z \times h_2 Z \times \cdots \times h_n Z \). Note that the real point (0,...,0) is mapped onto the digital point (0,...,0).

Description of template class 'GaussDigitizer'

GaussDigitizer is a model of CDigitalEuclideanShape and CDigitalBoundedShape. It is thus a model of CPointPredicate. A Gauss digitizer owns a RegularPointEmbedder, a model of CPointEmbedder.

Template Parameters:

TSpace	the type of digital Space where the digitized object lies.
TEuclideanShape	a model of CEuclideanOrientedShape and CEuclideanBoundedShape

Examples:: topology/frontierAndBoundary.cpp.

Definition at line 77 of file GaussDigitizer.h.

Member Typedef Documentation

template<typename TSpace, typename TEuclideanShape>

typedef HyperRectDomain<Space> DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Domain

Definition at line 88 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef TEuclideanShape DGtal::GaussDigitizer< TSpace, TEuclideanShape >::EuclideanShape

Definition at line 87 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef Space::Integer DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Integer

Definition at line 82 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef Space::Point DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Point

Definition at line 83 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef RegularPointEmbedder<Space> DGtal::GaussDigitizer< TSpace, TEuclideanShape >::PointEmbedder

Definition at line 89 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef Space::RealPoint DGtal::GaussDigitizer< TSpace, TEuclideanShape >::RealPoint

Definition at line 85 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef Space::RealPoint DGtal::GaussDigitizer< TSpace, TEuclideanShape >::RealVector

Definition at line 86 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef TSpace DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Space

Definition at line 81 of file GaussDigitizer.h.

template<typename TSpace, typename TEuclideanShape>

typedef Space::Vector DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Vector

Definition at line 84 of file GaussDigitizer.h.

Constructor & Destructor Documentation

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::~GaussDigitizer ( )

inline

Destructor.

Definition at line 46 of file GaussDigitizer.ih.

{

}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::GaussDigitizer ( )

inline

Constructor. The object is not valid.

Definition at line 52 of file GaussDigitizer.ih.

: myEShape( 0 )

{}

Member Function Documentation

template<typename TSpace , typename TEuclideanShape >

void DGtal::GaussDigitizer< TSpace, TEuclideanShape >::attach ( const EuclideanShape & shape )

inline

Parameters:

shape the digitizer now references the given shape.

Examples:: topology/frontierAndBoundary.cpp.

Definition at line 76 of file GaussDigitizer.ih.

Referenced by DGtal::Shapes< TDomain >::euclideanShaper().

{
  myEShape = &shape;
}

template<typename TSpace, typename TEuclideanShape>

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::BOOST_CONCEPT_ASSERT ( (CEuclideanOrientedShape< TEuclideanShape >) )

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Point DGtal::GaussDigitizer< TSpace, TEuclideanShape >::ceil ( const RealPoint & p ) const

inline

Parameters:

p	any point in the Euclidean space.

Returns:: the digital point ceil( p / gridSteps ).

Definition at line 138 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::ceil().

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::ceil().

{
  return myPointEmbedder.ceil( p );
}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::RealPoint DGtal::GaussDigitizer< TSpace, TEuclideanShape >::embed ( const Point & p ) const

inline

Map a digital point to its corresponding point in the Eucldiean space.

Parameters:

p	any digital point in the digital space.

Returns:: its centroid embedding in the Euclidean space.

Definition at line 156 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::embed().

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::embed(), and DGtal::GaussDigitizer< TSpace, TEuclideanShape >::orientation().

{
  return myPointEmbedder.embed( p );
}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Point DGtal::GaussDigitizer< TSpace, TEuclideanShape >::floor ( const RealPoint & p ) const

inline

Parameters:

p	any point in the Euclidean space.

Returns:: the digital point floor( p / gridSteps ).

Definition at line 129 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::floor().

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::floor().

{
  return myPointEmbedder.floor( p );
}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Domain DGtal::GaussDigitizer< TSpace, TEuclideanShape >::getDomain ( ) const

inline

Returns:: the domain chosen for the digitizer.

See also:: init

Examples:: topology/frontierAndBoundary.cpp.

Definition at line 119 of file GaussDigitizer.ih.

{
  return Domain( getLowerBound(), getUpperBound() );
}

template<typename TSpace , typename TEuclideanShape >

const DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Point & DGtal::GaussDigitizer< TSpace, TEuclideanShape >::getLowerBound ( ) const

inline

Returns:: the lowest admissible digital point.

See also:: init

Definition at line 175 of file GaussDigitizer.ih.

{
  return myLowerPoint;
}

template<typename TSpace , typename TEuclideanShape >

const DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Point & DGtal::GaussDigitizer< TSpace, TEuclideanShape >::getUpperBound ( ) const

inline

Returns:: the highest admissible digital point.

See also:: init

Definition at line 184 of file GaussDigitizer.ih.

{
  return myUpperPoint;
}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::RealVector DGtal::GaussDigitizer< TSpace, TEuclideanShape >::gridSteps ( ) const

inline

Returns:: the grid steps in each direction.

Definition at line 202 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::gridSteps().

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::gridSteps().

{
  return myPointEmbedder.gridSteps();
}

template<typename TSpace , typename TEuclideanShape >

void DGtal::GaussDigitizer< TSpace, TEuclideanShape >::init	(	const RealPoint &	xLow,
		const RealPoint &	xUp,
		typename RealVector::Component	gridStep
	)

inline

Initializes the digital bounds of the digitizer so as to cover at least the space specified by [xLow] and [xUp]. The real value [gridStep] specifies the same grid step in every direction.

Parameters:

xLow	Euclidean lower bound for the digitizer.
xUp	Euclidean upper bound for the digitizer.
gridStep	the grid step (distance between two embedded adjacent digital points) identical in every direction.

Examples:: topology/frontierAndBoundary.cpp.

Definition at line 85 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::init().

Referenced by DGtal::Shapes< TDomain >::euclideanShaper(), and DGtal::GaussDigitizer< TSpace, TEuclideanShape >::init().

{
  myPointEmbedder.init( gridStep );
  myLowerPoint = myPointEmbedder.floor( xLow );
  myUpperPoint = myPointEmbedder.ceil( xUp );
}

template<typename TSpace , typename TEuclideanShape >

void DGtal::GaussDigitizer< TSpace, TEuclideanShape >::init	(	const RealPoint &	xLow,
		const RealPoint &	xUp,
		const RealVector &	gridSteps
	)

inline

Initializes the digital bounds of the digitizer so as to cover at least the space specified by [xLow] and [xUp]. The real vector [gridSteps] specifies the grid steps in each direction.

Parameters:

xLow	Euclidean lower bound for the digitizer.
xUp	Euclidean upper bound for the digitizer.
gridSteps	the grid steps in each direction.

Definition at line 97 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::init().

{
  myPointEmbedder.init( aGridSteps );
  myLowerPoint = myPointEmbedder.floor( xLow );
  myUpperPoint = myPointEmbedder.ceil( xUp );
}

template<typename TSpace , typename TEuclideanShape >

bool DGtal::GaussDigitizer< TSpace, TEuclideanShape >::isValid ( ) const

inline

Checks the validity/consistency of the object.

Returns:: 'true' if the object is valid, 'false' otherwise.

Definition at line 230 of file GaussDigitizer.ih.

{
    return true;
}

template<typename TSpace , typename TEuclideanShape >

bool DGtal::GaussDigitizer< TSpace, TEuclideanShape >::operator() ( const Point & p ) const

inline

Parameters:

p	any point in the digital plane.

Returns:: 'true' if the point is inside the shape, 'false' if it is strictly outside.

Definition at line 165 of file GaussDigitizer.ih.

References DGtal::INSIDE.

{
  ASSERT( myEShape != 0 );
  return (myEShape->orientation( embed( p ) ) == INSIDE);
}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape > & DGtal::GaussDigitizer< TSpace, TEuclideanShape >::operator= ( const GaussDigitizer< TSpace, TEuclideanShape > & other )

inline

Assignment. Required by CPointPredicate.

Parameters:

other the object to copy.

Returns:: a reference on 'this'.

Definition at line 60 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myEShape, DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myLowerPoint, DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myPointEmbedder, and DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myUpperPoint.

{
  if ( this != &other )
    {
      myEShape = other.myEShape;
      myPointEmbedder = other.myPointEmbedder;
      myLowerPoint = other.myLowerPoint;
      myUpperPoint = other.myUpperPoint;
    }
  return *this;
}

template<typename TSpace, typename TEuclideanShape>

Orientation DGtal::GaussDigitizer< TSpace, TEuclideanShape >::orientation ( const Point & p ) const

inline

Orientation method to match with CDigitalOrientedShape concept.

Parameters:

p	a digital point

Returns:: negative orientation if the point is inside the shape, 0 if it is on the shape and positive orientation otherwise.

Definition at line 196 of file GaussDigitizer.h.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::embed(), and DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myEShape.

    { 
      return myEShape->orientation(embed(p));
    }

template<typename TSpace , typename TEuclideanShape >

const DGtal::GaussDigitizer< TSpace, TEuclideanShape >::PointEmbedder & DGtal::GaussDigitizer< TSpace, TEuclideanShape >::pointEmbedder ( ) const

inline

Returns:: the associated point embedder.

Definition at line 110 of file GaussDigitizer.ih.

{
  return myPointEmbedder;
}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Vector DGtal::GaussDigitizer< TSpace, TEuclideanShape >::resolution ( ) const

inline

Returns:: the resolution in each direction.

Definition at line 193 of file GaussDigitizer.ih.

{
  return getUpperBound() - getLowerBound();
}

template<typename TSpace , typename TEuclideanShape >

DGtal::GaussDigitizer< TSpace, TEuclideanShape >::Point DGtal::GaussDigitizer< TSpace, TEuclideanShape >::round ( const RealPoint & p ) const

inline

Parameters:

p	any point in the Euclidean space.

Returns:: the digital point round( p / gridSteps ), i.e. the "closest" digital point.

Definition at line 147 of file GaussDigitizer.ih.

References DGtal::GaussDigitizer< TSpace, TEuclideanShape >::round().

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::round().

{
  return myPointEmbedder.round( p );
}

template<typename TSpace , typename TEuclideanShape >

void DGtal::GaussDigitizer< TSpace, TEuclideanShape >::selfDisplay ( std::ostream & out ) const

inline

Writes/Displays the object on an output stream.

Parameters:

out	the output stream where the object is written.

Definition at line 218 of file GaussDigitizer.ih.

{
  out << "[GaussDigitizer]";
}

Field Documentation

template<typename TSpace, typename TEuclideanShape>

const EuclideanShape* DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myEShape

protected

The referenced shape or 0 if not initialized.

Definition at line 250 of file GaussDigitizer.h.

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::operator=(), and DGtal::GaussDigitizer< TSpace, TEuclideanShape >::orientation().

template<typename TSpace, typename TEuclideanShape>

Point DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myLowerPoint

protected

Digital lowest point.

Definition at line 256 of file GaussDigitizer.h.

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::operator=().

template<typename TSpace, typename TEuclideanShape>

RegularPointEmbedder<Space> DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myPointEmbedder

protected

The embedder.

Definition at line 253 of file GaussDigitizer.h.

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::operator=().

template<typename TSpace, typename TEuclideanShape>

Point DGtal::GaussDigitizer< TSpace, TEuclideanShape >::myUpperPoint

protected

Digital uppest point.

Definition at line 259 of file GaussDigitizer.h.

Referenced by DGtal::GaussDigitizer< TSpace, TEuclideanShape >::operator=().

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Protected Attributes

Detailed Description

template<typename TSpace, typename TEuclideanShape> class DGtal::GaussDigitizer< TSpace, TEuclideanShape >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Field Documentation

template<typename TSpace, typename TEuclideanShape>
class DGtal::GaussDigitizer< TSpace, TEuclideanShape >