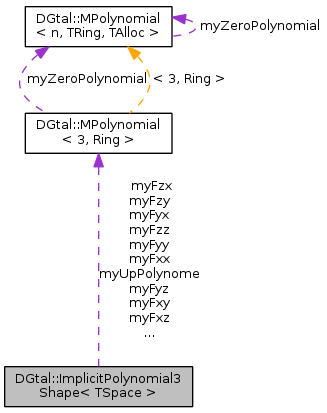
#include <ImplicitPolynomial3Shape.h>

Collaboration diagram for DGtal::ImplicitPolynomial3Shape< TSpace >:

Public Types
typedef ImplicitPolynomial3Shape < TSpace >	Self
typedef TSpace	Space
typedef Space::RealPoint	RealPoint
typedef Space::RealVector	RealVector
typedef RealPoint::Coordinate	Ring
typedef Space::Integer	Integer
typedef MPolynomial< 3, Ring >	Polynomial3
typedef Ring	Value

Public Member Functions
	BOOST_STATIC_ASSERT ((Space::dimension==3))
	ImplicitPolynomial3Shape (const Polynomial3 &poly)
ImplicitPolynomial3Shape &	operator= (const ImplicitPolynomial3Shape &other)
	~ImplicitPolynomial3Shape ()
void	init (const Polynomial3 &poly)
double	operator() (const RealPoint &aPoint) const
bool	isInside (const RealPoint &aPoint) const
Orientation	orientation (const RealPoint &aPoint) const
RealVector	gradient (const RealPoint &aPoint) const
double	meanCurvature (const RealPoint &aPoint) const
double	gaussianCurvature (const RealPoint &aPoint) const
RealPoint	nearestPoint (const RealPoint &aPoint, const double accuracy, const int maxIter, const double gamma) const
void	selfDisplay (std::ostream &out) const
bool	isValid () const

Protected Member Functions
	ImplicitPolynomial3Shape ()

Detailed Description

template<typename TSpace>
class DGtal::ImplicitPolynomial3Shape< TSpace >

Aim: model of CEuclideanOrientedShape concepts to create a shape from a polynomial.

Description of template class 'ImplicitPolynomial3Shape'

Model of CImplicitFunction

Template Parameters:

TSpace the Digital space definition.

Definition at line 67 of file ImplicitPolynomial3Shape.h.

Member Typedef Documentation

template<typename TSpace>

typedef Space::Integer DGtal::ImplicitPolynomial3Shape< TSpace >::Integer

Definition at line 76 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

typedef MPolynomial< 3, Ring > DGtal::ImplicitPolynomial3Shape< TSpace >::Polynomial3

Definition at line 77 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

typedef Space::RealPoint DGtal::ImplicitPolynomial3Shape< TSpace >::RealPoint

Definition at line 73 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

typedef Space::RealVector DGtal::ImplicitPolynomial3Shape< TSpace >::RealVector

Definition at line 74 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

typedef RealPoint::Coordinate DGtal::ImplicitPolynomial3Shape< TSpace >::Ring

Definition at line 75 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

typedef ImplicitPolynomial3Shape<TSpace> DGtal::ImplicitPolynomial3Shape< TSpace >::Self

Definition at line 71 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

typedef TSpace DGtal::ImplicitPolynomial3Shape< TSpace >::Space

Definition at line 72 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

typedef Ring DGtal::ImplicitPolynomial3Shape< TSpace >::Value

Definition at line 78 of file ImplicitPolynomial3Shape.h.

Constructor & Destructor Documentation

template<typename TSpace >

DGtal::ImplicitPolynomial3Shape< TSpace >::ImplicitPolynomial3Shape ( const Polynomial3 & poly )

inline

Constructor from an arbitrary polynomial.

Parameters:

poly	any multivariate polynomial (the number of variables is the dimension of the space)

Definition at line 51 of file ImplicitPolynomial3Shape.ih.

{
  init( poly );
}

template<typename TSpace >

DGtal::ImplicitPolynomial3Shape< TSpace >::~ImplicitPolynomial3Shape ( )

inline

Destructor.

Definition at line 44 of file ImplicitPolynomial3Shape.ih.

{

}

template<typename TSpace>

DGtal::ImplicitPolynomial3Shape< TSpace >::ImplicitPolynomial3Shape ( )

protected

Constructor. Forbidden by default (protected to avoid g++ warnings).

Member Function Documentation

template<typename TSpace>

DGtal::ImplicitPolynomial3Shape< TSpace >::BOOST_STATIC_ASSERT ( (Space::dimension==3) )

template<typename TSpace >

double DGtal::ImplicitPolynomial3Shape< TSpace >::gaussianCurvature ( const RealPoint & aPoint ) const

inline

Gaussian curvature estimation at aPoint

Precondition:: aPoint must be close to the surface.

Parameters:

aPoint any point in the Euclidean space.

Returns:: the gaussian curvature value of the polynomial at aPoint.

Definition at line 200 of file ImplicitPolynomial3Shape.ih.

{
  double vFx= myFx( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFy= myFy( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFz= myFz( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFxx= myFxx( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFxy= myFxy( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFxz= myFxz( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  //double vFyx= myFyx( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFyy= myFyy( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFyz= myFyz( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  
  /*double vFzx = myFzx( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  double vFzy = myFzy( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  */
  double vFzz = myFzz( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
 
  double A = vFz*(vFxx*vFz-2.0*vFx*vFxz)+vFx*vFx*vFzz;
  double B = vFz*(vFyy*vFz-2.0*vFy*vFyz)+vFy*vFy*vFzz;
  double C = vFz*(-vFx*vFyz+vFxy*vFz-vFxz*vFy)+vFx*vFy*vFzz;
  double D = vFz*(vFx*vFx+vFy*vFy+vFz*vFz);
  double G= (A*B-C*C)/(D*D);
  return G;
}

template<typename TSpace >

DGtal::ImplicitPolynomial3Shape< TSpace >::RealVector DGtal::ImplicitPolynomial3Shape< TSpace >::gradient ( const RealPoint & aPoint ) const

inline

Parameters:

aPoint any point in the Euclidean space.

Returns:: the gradient vector of the polynomial at aPoint.

Definition at line 154 of file ImplicitPolynomial3Shape.ih.

{
  // ISO C++ tells that an object created at return time will not be
  // copied into the caller context, but will be already defined in
  // the correct context.
  return RealVector
      ( myFx ( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] ),
        myFy ( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] ),
        myFz ( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] ) );
}

template<typename TSpace >

void DGtal::ImplicitPolynomial3Shape< TSpace >::init ( const Polynomial3 & poly )

inline

Initialize from an arbitrary polynomial.

Parameters:

poly	any multivariate polynomial (the number of variables is the dimension of the space)

Definition at line 89 of file ImplicitPolynomial3Shape.ih.

{
  myPolynomial = poly;
  myFx= derivative<0>( poly );
  myFy= derivative<1>( poly );
  myFz= derivative<2>( poly );
  myFxx= derivative<0>( myFx );
  myFxy= derivative<1>( myFx );
  myFxz= derivative<2>( myFx);
  myFyx= derivative<0>( myFy );
  myFyy= derivative<1>( myFy );
  myFyz= derivative<2>( myFy );
  myFzx= derivative<0>( myFz );
  myFzy= derivative<1>( myFz );
  myFzz= derivative<2>( myFz );
  myUpPolynome = myFx*(myFx*myFxx+myFy*myFyx+myFz*myFzx)+
                                myFy*(myFx*myFxy+myFy*myFyy+myFz*myFzy)+
                                myFz*(myFx*myFxz+myFy*myFyz+myFz*myFzz)-
                                ( myFx*myFx +myFy*myFy+myFz*myFz )*(myFxx+myFyy+myFzz);
  myLowPolynome = myFx*myFx +myFy*myFy+myFz*myFz;
}

template<typename TSpace >

bool DGtal::ImplicitPolynomial3Shape< TSpace >::isInside ( const RealPoint & aPoint ) const

inline

Parameters:

aPoint any point in the Euclidean space.

Returns:: 'true' if the polynomial value is > 0.

Definition at line 130 of file ImplicitPolynomial3Shape.ih.

{
  return (this->operator()(aPoint) > (Ring)0);
}

template<typename TSpace >

bool DGtal::ImplicitPolynomial3Shape< TSpace >::isValid ( ) const

inline

Checks the validity/consistency of the object.

Returns:: 'true' if the object is valid, 'false' otherwise.

Definition at line 298 of file ImplicitPolynomial3Shape.ih.

{
  return true;
}

template<typename TSpace >

double DGtal::ImplicitPolynomial3Shape< TSpace >::meanCurvature ( const RealPoint & aPoint ) const

inline

Mean curvature estimation. This computation is based on the hessian formula of the mean curvature k=(∇F ∗ H (F ) ∗ ∇F T − |∇F |^2 *Trace(H (F ))/2|∇F |^3

Precondition:: a Point must be close to the surface.

Parameters:

aPoint any point in the Euclidean space.

Returns:: the mean curvature value of the polynomial at aPoint.

Parameters:

aPoint any point in the Euclidean space. This computation is based on the hessian formula of the mean curvature k=-(∇F ∗ H (F ) ∗ ∇F T − |∇F |^2 *Trace(H (F ))/2|∇F |^3 we define it as positive for a sphere

Returns:: the mean curvature value of the polynomial at aPoint.

Definition at line 182 of file ImplicitPolynomial3Shape.ih.

{
  double temp= myLowPolynome( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  temp = sqrt(temp);
  double downValue = 2*(temp*temp*temp);
  double upValue = myUpPolynome( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
  return -(upValue/downValue);
}

template<typename TSpace >

DGtal::ImplicitPolynomial3Shape< TSpace >::RealPoint DGtal::ImplicitPolynomial3Shape< TSpace >::nearestPoint	(	const RealPoint &	aPoint,
		const double	accuracy,
		const int	maxIter,
		const double	gamma
	)		const

inline

Perform a gradient descent in order to move a point aPoint closer to the implicit surface. More precisely, we use a sequence: x_n = x_(n-1) - gamma.gradient(x_(n-1). The descent is stopped if maxIter is reached or if |x_n - x_(n-1)| < accuracy.

Parameters:

aPoint	any point in the Euclidean space.
accuracy	distance criterion to stop the descent.
maxIter	fixes the maximum number of steps.
gamma	coefficient associated with the gradient.

Returns:: the nearest point on the surface to the one given in parameter.

Parameters:

aPoint	any point in the Euclidean space.
accuracy	refers to the precision
maxIter	refers to the maximum iterations the fonction user authorises
gamma	refers to the step This function is very useful for mean and gaussian curvature computation (If the set step is big) .For a small one ( <0.5) it's less usefull

Returns:: the nearest point on the surface to the one given in parameter.

Definition at line 249 of file ImplicitPolynomial3Shape.ih.

{
   RealPoint agradient= (*this).gradient(aPoint);
   RealPoint X=aPoint;
   int numberIter=0;
   while((fabs((*this)(X))>=accuracy) && (numberIter<maxIter))
   {
        double norm=agradient.norm();
        RealPoint normalizedGradient= RealPoint(agradient[0]/norm,agradient[1]/norm,agradient[2]/norm);
        double alpha =gamma;
        if((*this)(X)>0)
        {
                alpha=-alpha;
        }
        else
        {
        }
        
        X=X+normalizedGradient*alpha;
        agradient=  (*this).gradient(X);
        numberIter++;
   }
        return X;
}

template<typename TSpace >

double DGtal::ImplicitPolynomial3Shape< TSpace >::operator() ( const RealPoint & aPoint ) const

inline

Parameters:

aPoint any point in the Euclidean space.

Returns:: the value of the polynomial at aPoint.

Definition at line 121 of file ImplicitPolynomial3Shape.ih.

{
  return myPolynomial( aPoint[ 0 ] )( aPoint[ 1 ] )( aPoint[ 2 ] );
}

template<typename TSpace >

DGtal::ImplicitPolynomial3Shape< TSpace > & DGtal::ImplicitPolynomial3Shape< TSpace >::operator= ( const ImplicitPolynomial3Shape< TSpace > & other )

inline

Assignment.

Parameters:

other the object to copy.

Returns:: a reference on 'this'.

Definition at line 60 of file ImplicitPolynomial3Shape.ih.

{
  if ( this != &other )
  {
    myPolynomial = other.myPolynomial;
    myFx= other.myFx;
    myFy= other.myFy;
    myFz= other.myFz;
    myFxx= other.myFxx;
    myFxy= other.myFxy;
    myFxz= other.myFxz;
    myFyx= other.myFyx;
    myFyy= other.myFyy;
    myFyz= other.myFyz;
    myFzx= other.myFzx;
    myFzy= other.myFzy;
    myFzz= other.myFzz;
  }
  return *this;
}

template<typename TSpace >

DGtal::Orientation DGtal::ImplicitPolynomial3Shape< TSpace >::orientation ( const RealPoint & aPoint ) const

inline

Parameters:

aPoint any point in the Euclidean space.

Returns:: INSIDE if the polynomial value is > 0, OUTSIDE if < 0, ON otherwise.

Definition at line 139 of file ImplicitPolynomial3Shape.ih.

References DGtal::INSIDE, DGtal::ON, and DGtal::OUTSIDE.

{
  Ring v = this->operator()(aPoint);
  if ( v > (Ring)0 )
    return INSIDE;
  else if ( v < (Ring)0 )
    return OUTSIDE;
  else
    return ON;
}

template<typename TSpace >

void DGtal::ImplicitPolynomial3Shape< TSpace >::selfDisplay ( std::ostream & out ) const

inline

Writes/Displays the object on an output stream.

Parameters:

out	the output stream where the object is written.

Definition at line 286 of file ImplicitPolynomial3Shape.ih.

{
  out << "[ImplicitPolynomial3Shape] P(x,y,z) = " << myPolynomial;
}

Field Documentation

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFx

private

Definition at line 210 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFxx

private

Definition at line 214 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFxy

private

Definition at line 215 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFxz

private

Definition at line 216 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFy

private

Definition at line 211 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFyx

private

Definition at line 218 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFyy

private

Definition at line 219 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFyz

private

Definition at line 220 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFz

private

Definition at line 212 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFzx

private

Definition at line 222 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFzy

private

Definition at line 223 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myFzz

private

Definition at line 224 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myLowPolynome

private

Definition at line 229 of file ImplicitPolynomial3Shape.h.

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myPolynomial

private

The 3-polynomial defining the implicit shape.

Definition at line 207 of file ImplicitPolynomial3Shape.h.

Referenced by DGtal::ImplicitPolynomial3Shape< TSpace >::operator=().

template<typename TSpace>

Polynomial3 DGtal::ImplicitPolynomial3Shape< TSpace >::myUpPolynome

private

Definition at line 228 of file ImplicitPolynomial3Shape.h.

The documentation for this class was generated from the following files:

Private Attributes
Polynomial3	myPolynomial
Polynomial3	myFx
Polynomial3	myFy
Polynomial3	myFz
Polynomial3	myFxx
Polynomial3	myFxy
Polynomial3	myFxz
Polynomial3	myFyx
Polynomial3	myFyy
Polynomial3	myFyz
Polynomial3	myFzx
Polynomial3	myFzy
Polynomial3	myFzz
Polynomial3	myUpPolynome
Polynomial3	myLowPolynome

Public Types

Public Member Functions

Protected Member Functions

Private Attributes

Detailed Description

template<typename TSpace> class DGtal::ImplicitPolynomial3Shape< TSpace >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Field Documentation

template<typename TSpace>
class DGtal::ImplicitPolynomial3Shape< TSpace >