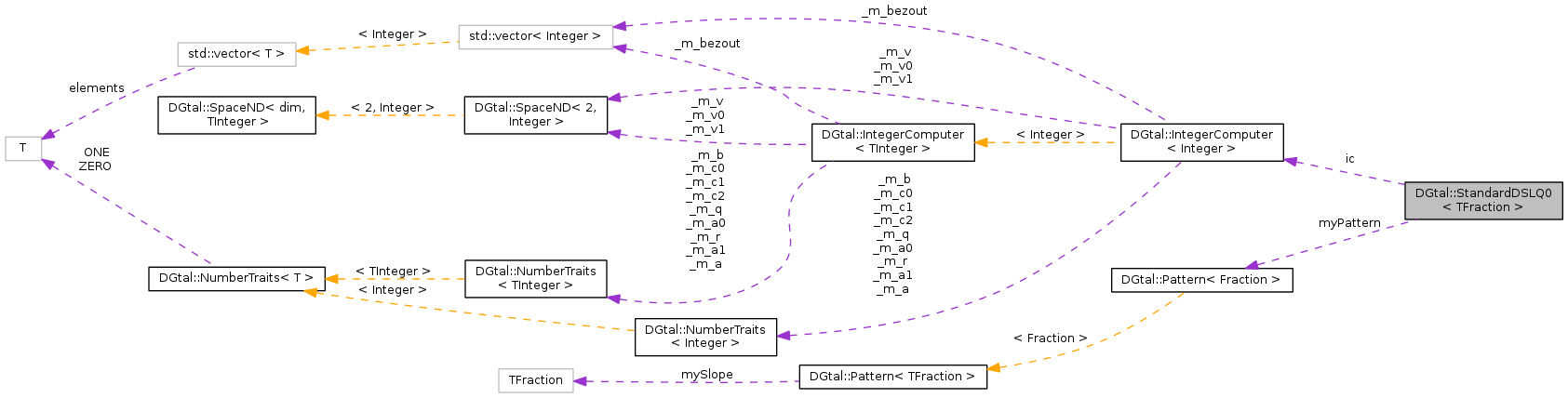
#include <StandardDSLQ0.h>

Collaboration diagram for DGtal::StandardDSLQ0< TFraction >:

Data Structures
struct	ConstIterator

Public Types
typedef TFraction	Fraction
typedef StandardDSLQ0< TFraction >	Self
typedef Fraction::Integer	Integer
typedef Fraction::UnsignedInteger	UnsignedInteger
typedef Fraction::Quotient	Quotient
typedef IntegerComputer< Integer >	IC
typedef IC::IntegerParamType	IntegerParamType
typedef IC::Vector2I	Vector2I
typedef IC::Point2I	Point2I
typedef IC::Point2I	Point

Public Member Functions
	~StandardDSLQ0 ()
	StandardDSLQ0 ()
	StandardDSLQ0 (const StandardDSLQ0 &other)
StandardDSLQ0 &	operator= (const StandardDSLQ0 &other)
	StandardDSLQ0 (Fraction aSlope, IntegerParamType aMu)
	StandardDSLQ0 (IntegerParamType a1, IntegerParamType b1, IntegerParamType mu1)
bool	operator() (const Point &p) const
Fraction	slope () const
const Integer &	mu () const
Integer	mup () const
Integer	a () const
Integer	b () const
Vector2I	v () const
ConstIterator	begin (Point p) const
ConstIterator	end (Point p) const
const Pattern< Fraction > &	pattern () const
Integer	r (const Point &p) const
Point	U () const
Point	L () const
Point	lowestY (IntegerParamType x) const
Point	uppermostY (IntegerParamType x) const
Point	lowestX (IntegerParamType y) const
Point	uppermostX (IntegerParamType y) const
bool	before (const Point &p1, const Point &p2) const
bool	beforeOrEqual (const Point &p1, const Point &p2) const
Self	reversedSmartDSS (const Point &A, const Point &B) const
Self	reversedSmartDSS (Point U1, Point U2, const Point &A, const Point &B) const
Self	DSSWithinTwoPatterns (Point U1, Point U2, const Point &A, const Point &B) const
Self	smartDSS (const Point &A, const Point &B) const
void	selfDisplay (std::ostream &out) const
bool	isValid () const

Protected Attributes
Pattern< Fraction >	myPattern
Integer	myMu

Static Private Member Functions
static Fraction	deepest (Fraction f1, Fraction f2, Fraction f3)
static Fraction	deepest (Fraction f1, Fraction f2)

Private Attributes
IC	ic

Detailed Description

template<typename TFraction>
class DGtal::StandardDSLQ0< TFraction >

Definition at line 78 of file StandardDSLQ0.h.

Member Typedef Documentation

template<typename TFraction>

typedef TFraction DGtal::StandardDSLQ0< TFraction >::Fraction

Definition at line 82 of file StandardDSLQ0.h.

template<typename TFraction>

typedef IntegerComputer<Integer> DGtal::StandardDSLQ0< TFraction >::IC

Definition at line 90 of file StandardDSLQ0.h.

template<typename TFraction>

typedef Fraction::Integer DGtal::StandardDSLQ0< TFraction >::Integer

Definition at line 84 of file StandardDSLQ0.h.

template<typename TFraction>

typedef IC::IntegerParamType DGtal::StandardDSLQ0< TFraction >::IntegerParamType

Definition at line 91 of file StandardDSLQ0.h.

template<typename TFraction>

typedef IC::Point2I DGtal::StandardDSLQ0< TFraction >::Point

Definition at line 96 of file StandardDSLQ0.h.

template<typename TFraction>

typedef IC::Point2I DGtal::StandardDSLQ0< TFraction >::Point2I

Definition at line 93 of file StandardDSLQ0.h.

template<typename TFraction>

typedef Fraction::Quotient DGtal::StandardDSLQ0< TFraction >::Quotient

Definition at line 86 of file StandardDSLQ0.h.

template<typename TFraction>

typedef StandardDSLQ0<TFraction> DGtal::StandardDSLQ0< TFraction >::Self

Definition at line 83 of file StandardDSLQ0.h.

template<typename TFraction>

typedef Fraction::UnsignedInteger DGtal::StandardDSLQ0< TFraction >::UnsignedInteger

Definition at line 85 of file StandardDSLQ0.h.

template<typename TFraction>

typedef IC::Vector2I DGtal::StandardDSLQ0< TFraction >::Vector2I

Definition at line 92 of file StandardDSLQ0.h.

Constructor & Destructor Documentation

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::~StandardDSLQ0 ( )

inline

Destructor.

Definition at line 45 of file StandardDSLQ0.ih.

{

}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::StandardDSLQ0 ( )

inline

Constructor. Null DSL.

Definition at line 52 of file StandardDSLQ0.ih.

  : myPattern()
{
}

template<typename TFraction>

DGtal::StandardDSLQ0< TFraction >::StandardDSLQ0 ( const StandardDSLQ0< TFraction > & other )

Copy constructor.

Parameters:

other the object to clone.

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::StandardDSLQ0	(	Fraction	aSlope,
		IntegerParamType	aMu
	)

inline

Creates the DSL(a,b,mu).

Parameters:

aSlope	the slope a/b, where gcd(a,b)=1
aMu	the shift to origin.

Definition at line 79 of file StandardDSLQ0.ih.

  : myPattern( aSlope ), myMu( aMu )
{
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::StandardDSLQ0	(	IntegerParamType	a1,
		IntegerParamType	b1,
		IntegerParamType	mu1
	)

inline

Creates the DSL(a/g,b/g,mu), where g = gcd( a, b).

Parameters:

a1	any integer
b1	any integer
mu1	the shift to origin.

Definition at line 87 of file StandardDSLQ0.ih.

  : myPattern( a1, b1 ), myMu( mu1 )
{
}

Member Function Documentation

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Integer DGtal::StandardDSLQ0< TFraction >::a ( ) const

inline

Returns:: a the numerator of the slope.

Definition at line 153 of file StandardDSLQ0.ih.

{
  return slope().p();
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Integer DGtal::StandardDSLQ0< TFraction >::b ( ) const

inline

Returns:: b the denominator of the slope.

Definition at line 162 of file StandardDSLQ0.ih.

{
  return slope().q();
}

template<typename TFraction >

bool DGtal::StandardDSLQ0< TFraction >::before	(	const Point &	p1,
		const Point &	p2
	)		const

inline

Returns:: true if p1 is before p2 in the DSL.

Definition at line 242 of file StandardDSLQ0.ih.

{
  return ( p1[ 0 ] < p2[ 0 ] )
    || ( ( p1[ 0 ] == p2[ 0 ] ) && ( p1[ 1 ] < p2[ 1 ] ) );
}

template<typename TFraction >

bool DGtal::StandardDSLQ0< TFraction >::beforeOrEqual	(	const Point &	p1,
		const Point &	p2
	)		const

inline

Returns:: true if p1 is before or equal to p2 in the DSL.

Definition at line 252 of file StandardDSLQ0.ih.

{
  return ( p1[ 0 ] < p2[ 0 ] )
    || ( ( p1[ 0 ] == p2[ 0 ] ) && ( p1[ 1 ] <= p2[ 1 ] ) );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::ConstIterator DGtal::StandardDSLQ0< TFraction >::begin ( Point p ) const

Parameters:

p	a point in the DSL.

Returns:: an iterator on the DSL pointing on p.

Definition at line 261 of file StandardDSLQ0.ih.

{
  return ConstIterator( *this, p );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Fraction DGtal::StandardDSLQ0< TFraction >::deepest	(	Fraction	f1,
		Fraction	f2,
		Fraction	f3
	)

inlinestaticprivate

Definition at line 592 of file StandardDSLQ0.ih.

{
  return deepest( f1, deepest( f2, f3 ) ); 
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Fraction DGtal::StandardDSLQ0< TFraction >::deepest	(	Fraction	f1,
		Fraction	f2
	)

inlinestaticprivate

Definition at line 601 of file StandardDSLQ0.ih.

{
  return ( ( f1.k() > f2.k() ) 
           || ( ( f1.k() == f2.k() ) && ( f1.u() >= f2.u() ) ) )
    ? f1 : f2;
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Self DGtal::StandardDSLQ0< TFraction >::DSSWithinTwoPatterns	(	Point	U1,
		Point	U2,
		const Point &	A,
		const Point &	B
	)		const

Used by reversedSmartDSS. Computes the exact characteristics of the subsegment [A,B] of this DSL. Note that |U2-U1| = 2 * length().

Parameters:

A	any point belonging to this DSL, A < B.
B	any point belonging to this DSL, A < B.
U1	the first upper leaning point such that U1 <= A.
U2	the second upper leaning point such that B <= U2.

Returns:: the minimal DSL containing [A,B].

Definition at line 383 of file StandardDSLQ0.ih.

References DGtal::Pattern< TFraction >::getGreatestIncludedSubpattern(), DGtal::Pattern< TFraction >::getSmallestCoveringSubpattern(), DGtal::Pattern< TFraction >::L(), DGtal::Pattern< TFraction >::length(), DGtal::Pattern< TFraction >::rE(), DGtal::Pattern< TFraction >::slope(), DGtal::Pattern< TFraction >::v(), and DGtal::StandardDSLQ0< TFraction >::v().

{
  Integer posA, posB;
  Point Um = U1 + pattern().v();
  ASSERT( Um + pattern().v() == U2 );
  ASSERT( before( A, B ) );
  ASSERT( before( A, Um ) );
  ASSERT( before( Um, B ) );
  ASSERT( r( U1 ) == mu() && r( U2 ) == mu() );
  bool readyLU = false;
  bool readyRU = false;
  bool readyL = false;
  Point L1 = U1 + pattern().L( 0 );
  Point L2 = L1 + pattern().v();
  Pattern<Fraction> subpattern;
  Pattern<Fraction> patDeepest;
  Pattern<Fraction> patLU = pattern();
  Pattern<Fraction> patRU = pattern();
  Pattern<Fraction> patL = pattern();
  Quotient nb;
  Vector2I startPos;
  #ifdef TRACE_DSL
  std::cerr << "[DSSWithinTwoPatterns] " << (*this) 
            << " " << pattern().rE() << std::endl
            << "  +- U1=" << U1 << " A=" << A 
            << " B=" << B << " U2=" << U2 
            << " L1=" << L1 << std::endl;
  #endif
  while( true ) //for ( Quotient i = NumberTraits<Quotient>::ZERO; i <= pattern().slope().k(); ++i )
    {
      if ( ! readyLU )
        {
          bool mLU = patLU.getSmallestCoveringSubpattern
            ( subpattern, nb, startPos,
              ( A - U1 ).norm1(), ( Um - U1 ).norm1(), false );
          if ( ! mLU || nb > 1 )
            {
              bool n = patLU.getGreatestIncludedSubpattern
                ( subpattern, nb, startPos, 
                  ( A - U1 ).norm1(), ( Um - U1 ).norm1(), false );
              ASSERT( n );
              readyLU = true;
            }
          patLU = subpattern;
          U1 += startPos;
        }
      if ( ! readyRU )
        {
          bool mRU = patRU.getSmallestCoveringSubpattern
            ( subpattern, nb, startPos,
              0, ( B - Um ).norm1(), false );
          if ( ! mRU || nb > 1 )
            {
              bool n = patRU.getGreatestIncludedSubpattern
                ( subpattern, nb, startPos, 
                   0, ( B - Um ).norm1(), false );
              ASSERT( n );
              readyRU = true;
            }
          patRU = subpattern;
          ASSERT( ! patRU.slope().null() );
          U2 = Um + patRU.v() * nb;
        }
      if ( ! readyL )
        {
          posA = L1[ 0 ] <= A[ 0 ] ? ( A - L1 ).norm1() : 0;
          posB = L2[ 0 ] >  B[ 0 ] ? ( B - L1 ).norm1() : patL.length();
          bool mL = patL.getSmallestCoveringSubpattern
            ( subpattern, nb, startPos, posA, posB, true );
          if ( ! mL )
            {
              bool n = patL.getGreatestIncludedSubpattern
                ( subpattern, nb, startPos, posA, posB, true );
              ASSERT( n );
              patL = subpattern;
              readyL = true;
            }
          else
            { // One has to keep the pertinent pattern
              // It is the reversed pattern around Um.
              patL = subpattern;
              L2 = Um + patL.L( 0 );
              L1 = L2 - patL.v();
            }
          // patL = subpattern;
          // L1 += startPos;
          // L2 = L1 + patL.v() * nb;
        }
#ifdef TRACE_DSL
      std::cerr << "  (*) " << (readyLU ? '*' : '-')
                << "LU=" << patLU.rE() << " at " << U1 << std::endl;
      std::cerr << "  (*) " << (readyRU ? '*' : '-')
                << "RU=" << patRU.rE() << " til " << U2 << std::endl;
      std::cerr << "  (*) " << (readyL  ? '*' : '-')
                << "L =" << patL.rE()  << " at " << L1 << std::endl;
#endif
      if ( readyLU || readyRU || readyL )
        {
          patDeepest = deepest( patLU.slope(), patRU.slope(), patL.slope() );
#ifdef TRACE_DSL
          std::cerr << "      => deepest is " << patDeepest.rE() << std::endl;
#endif
        }
      if ( ( readyLU && patDeepest.slope().q() == patLU.slope().q() )
           || ( readyRU && patDeepest.slope().q() == patRU.slope().q() )
           || ( readyL  && patDeepest.slope().q() == patL.slope().q() ) )
        break;
    }
  Integer nmu = patDeepest.slope().p() * Um[ 0 ]
    - patDeepest.slope().q() * Um[ 1 ];
  return StandardDSLQ0( patDeepest.slope(), nmu );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::ConstIterator DGtal::StandardDSLQ0< TFraction >::end ( Point p ) const

Parameters:

p	a point in the DSL.

Returns:: an iterator on the DSL pointing after p.

Definition at line 269 of file StandardDSLQ0.ih.

{
  ConstIterator it( *this, p );
  return ++it;
}

template<typename TFraction >

bool DGtal::StandardDSLQ0< TFraction >::isValid ( ) const

inline

Checks the validity/consistency of the object.

Returns:: 'true' if the object is valid, 'false' otherwise.

Definition at line 631 of file StandardDSLQ0.ih.

{
    return true;
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Point DGtal::StandardDSLQ0< TFraction >::L ( ) const

inline

Returns:: the first lower leaning point of the DSL with greater x than U().

Definition at line 193 of file StandardDSLQ0.ih.

{
  return Point( U() + pattern().L( NumberTraits<Quotient>::ZERO ) );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Point DGtal::StandardDSLQ0< TFraction >::lowestX ( IntegerParamType y ) const

inline

Returns:: the point on this DSL with this y coordinate and lowest x coordinate.

Definition at line 222 of file StandardDSLQ0.ih.

{
  Integer q = mu() + b() * y;
  return Point( ic.ceilDiv( q, a() ), y );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Point DGtal::StandardDSLQ0< TFraction >::lowestY ( IntegerParamType x ) const

inline

Returns:: the point on this DSL with this x coordinate and lowest y coordinate.

Definition at line 202 of file StandardDSLQ0.ih.

{
  Integer q = a() * x - mup();
  return Point( x, ic.ceilDiv( q, b() ) );
}

template<typename TFraction >

const DGtal::StandardDSLQ0< TFraction >::Integer & DGtal::StandardDSLQ0< TFraction >::mu ( ) const

inline

Returns:: the shift to origin, which is also the lower diopantine constraint.

Definition at line 135 of file StandardDSLQ0.ih.

{
  return myMu;
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Integer DGtal::StandardDSLQ0< TFraction >::mup ( ) const

inline

Returns:: the upper diopantine constraint, ie. mu + a + b - 1

Definition at line 144 of file StandardDSLQ0.ih.

{
  return myMu + pattern().length() - NumberTraits<Integer>::ONE;
}

template<typename TFraction >

bool DGtal::StandardDSLQ0< TFraction >::operator() ( const Point & p ) const

inline

Parameters:

p	any point in Z2.

Returns:: 'true' iff the point p belongs to this.

Definition at line 96 of file StandardDSLQ0.ih.

{
  if ( slope().null() ) return false;
  Integer _r = r( p );
  return ( mu() <= _r ) && ( _r < ( mu() + pattern().length() ) );
}

template<typename TFraction>

DGtal::StandardDSLQ0< TFraction > & DGtal::StandardDSLQ0< TFraction >::operator= ( const StandardDSLQ0< TFraction > & other )

inline

Assignment.

Parameters:

other the object to copy.

Returns:: a reference on 'this'.

Definition at line 69 of file StandardDSLQ0.ih.

References DGtal::StandardDSLQ0< TFraction >::myMu, and DGtal::StandardDSLQ0< TFraction >::myPattern.

{
  myPattern = other.myPattern;
  myMu = other.myMu;
  return *this;
}

template<typename TFraction >

const DGtal::Pattern< TFraction > & DGtal::StandardDSLQ0< TFraction >::pattern ( ) const

inline

Returns:: the pattern of this DSL

Definition at line 126 of file StandardDSLQ0.ih.

{
  return myPattern;
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Integer DGtal::StandardDSLQ0< TFraction >::r ( const Point & p ) const

inline

Remainder a p.x - b p.y of point p in this DSL.

Parameters:

p	any point in Z2

Returns:: a p.x - b p.y

Definition at line 107 of file StandardDSLQ0.ih.

{
  ASSERT( ! slope().null() );
  return a() * p[ 0 ] - b() * p[ 1 ];
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Self DGtal::StandardDSLQ0< TFraction >::reversedSmartDSS	(	const Point &	A,
		const Point &	B
	)		const

Algorithm ReversedSmartDSS. See M. Said and J.-O. Lachaud, DGCI2010.

Computes the exact characteristics of the subsegment [A,B] of this DSL in time O(log(|B-A|)). An even better bound in the output is achieved.

Parameters:

A	any point belonging to this DSL, A < B.
B	any point belonging to this DSL, A < B.

Returns:: the minimal DSL containing [A,B].

Definition at line 279 of file StandardDSLQ0.ih.

Referenced by DGtal::StandardDSLQ0< TFraction >::reversedSmartDSS().

{
  Point _U = U();
  Integer cA = ic.floorDiv( A[ 0 ] - _U[ 0 ], v()[ 0 ] );
  Point U1 = _U + v() * cA;
  Integer cB = ic.ceilDiv( B[ 0 ] - _U[ 0 ], v()[ 0 ] );
  Point U2 = _U + v() * cB;
  if ( before( A, U1 ) ) U1 -= v();
  if ( before( U2, B ) ) U2 += v();
  return reversedSmartDSS( U1, U2, A, B );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Self DGtal::StandardDSLQ0< TFraction >::reversedSmartDSS	(	Point	U1,
		Point	U2,
		const Point &	A,
		const Point &	B
	)		const

Algorithm ReversedSmartDSS. See M. Said and J.-O. Lachaud, DGCI2010.

Computes the exact characteristics of the subsegment [A,B] of this DSL in time O(log(|B-A|)). An even better bound in the output is achieved.

Parameters:

A	any point belonging to this DSL, A < B.
B	any point belonging to this DSL, A < B.
U1	the first upper leaning point such that U1 <= A.
U2	the second upper leaning point such that B <= U2.

Returns:: the minimal DSL containing [A,B].

See also:: reversedSmartDSS( const Point & A, const Point & B )

Definition at line 295 of file StandardDSLQ0.ih.

References DGtal::Pattern< TFraction >::getSmallestCoveringSubpattern(), DGtal::Pattern< TFraction >::rE(), DGtal::StandardDSLQ0< TFraction >::reversedSmartDSS(), DGtal::Pattern< TFraction >::slope(), DGtal::Pattern< TFraction >::v(), and DGtal::StandardDSLQ0< TFraction >::v().

{
  #ifdef TRACE_DSL
  std::cerr << "[reversedSmartDSS] " << (*this) 
            << " " << pattern().rE() << std::endl
            << "  +- U1=" << U1 << " A=" << A 
            << " B=" << B << " U2=" << U2 << std::endl
            << " v()=" << pattern().v()
            << " u()=" << pattern().bezout()
            << " r(U())=" << r(U())
            << " mu=" << mu() << " r(U1)=" << r(U1)
            << " r(U2)=" << r(U2) 
            << " r(A)=" << r(A)
            << " r(B)=" << r(B)
            << " mup=" << mup()
            << " DSS(A)=" << this->operator()( A ) 
            << " DSS(B)=" << this->operator()( B ) << std::endl;
  #endif
  ASSERT( ! slope().null() );
  ASSERT( r( U1 ) == mu() && r( U2 ) == mu()
          && this->operator()( A ) && this->operator()( B ) );
  ASSERT( beforeOrEqual( U1, A ) );
  ASSERT( before( A, B ) );
  ASSERT( beforeOrEqual( B, U2 ) );
  if ( A[ 0 ] == B[ 0 ] ) return Self( 1, 0, A[ 0 ] );
  if ( A[ 1 ] == B[ 1 ] ) return Self( 0, 1, -A[ 1 ] );
  Integer dU = U2[ 0 ] - U1[ 0 ];
  ASSERT( dU >= b() );
#ifdef TRACE_DSL
  std::cerr << "  +- dU=" << dU << std::endl;
#endif
  if ( ( dU >= (3*b()) ) 
       || ( ( dU == (2*b()) ) && ( A == U1 || B == U2 ) )
       || ( A == U1 && B == U2 ) )
    {
#ifdef TRACE_DSL
      std::cerr << "[reversedSmartDSS] 3 patterns || ..." << std::endl;
#endif
      return *this;
    }
  // [A,B] is included in two patterns of this DSL.
  if ( dU == (2*b()) )
    {
#ifdef TRACE_DSL
      std::cerr << "[reversedSmartDSS] 2 patterns" << std::endl;
#endif
      return DSSWithinTwoPatterns( U1, U2, A, B );
    }
  // [A,B] is included in one patterns of this DSL.
  Pattern<Fraction> subpattern;
  Quotient nb;
  Vector2I startPos;
  Integer posA = ( A - U1 ).norm1();
  Integer posB = ( B - U1 ).norm1();
#ifdef TRACE_DSL
  std::cerr << "[reversedSmartDSS] 1 pattern" << std::endl;
#endif
  bool m = pattern().getSmallestCoveringSubpattern
    ( subpattern, nb, startPos, posA, posB );
#ifdef TRACE_DSL
  std::cerr << "  - smallest:" << subpattern.rE() << " at " << startPos << endl;
#endif
  if ( ! m )
    { // smallest covering subpattern is the pattern itself.
      bool n = pattern().getGreatestIncludedSubpattern
        ( subpattern, nb, startPos, posA, posB );
#ifdef TRACE_DSL
      std::cerr << "  - greatest:" << subpattern.rE() << " at " << startPos << endl;
#endif
      ASSERT( n );
      Point NU( U1 + startPos );
      Integer nmu = subpattern.slope().p() * NU[ 0 ]
        - subpattern.slope().q() * NU[ 1 ];
      return Self( subpattern.slope(), nmu );
    }
  // last case, recursive call.
  Point NU1( U1 + startPos );
  Point NU2( NU1 + subpattern.v()*nb );
  Integer nmu = subpattern.slope().p() * NU1[ 0 ]
    - subpattern.slope().q() * NU1[ 1 ];
  StandardDSLQ0 ndsl( subpattern.slope(), nmu );
  return ndsl.reversedSmartDSS( NU1, NU2, A, B );
}

template<typename TFraction >

void DGtal::StandardDSLQ0< TFraction >::selfDisplay ( std::ostream & out ) const

inline

Writes/Displays the object on an output stream.

Parameters:

out	the output stream where the object is written.

Definition at line 618 of file StandardDSLQ0.ih.

{
  out << "[StandardDSLQ0"
      << " a=" << a() << ", b=" << b() << ", mu=" << mu() << "]";
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Fraction DGtal::StandardDSLQ0< TFraction >::slope ( ) const

inline

Returns:: the slope of this DSL, an irreducible fraction

Definition at line 117 of file StandardDSLQ0.ih.

References DGtal::StandardDSLQ0< TFraction >::slope().

Referenced by DGtal::StandardDSLQ0< TFraction >::slope().

{
  return pattern().slope();
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Self DGtal::StandardDSLQ0< TFraction >::smartDSS	(	const Point &	A,
		const Point &	B
	)		const

Algorithm SmartDSS. See M. Said and J.-O. Lachaud, DGCI2009.

Computes the exact characteristics of the subsegment [A,B] of this DSL in time O(sum_k u_k), where the continued fraction of this DSL slope a/b is [u_0; u_1, u_2, ... ]

Parameters:

A	any point belonging to this DSL, A < B.
B	any point belonging to this DSL, A < B.

Returns:: the minimal DSL containing [A,B].

Definition at line 500 of file StandardDSLQ0.ih.

References DGtal::Pattern< TFraction >::bezout(), DGtal::Pattern< TFraction >::slope(), and DGtal::Pattern< TFraction >::v().

{
#ifdef TRACE_DSL
  std::cerr << "[smartDSS] " << (*this) 
            << " " << pattern().rE() << std::endl
            << " A=" << A << " B=" << B << std::endl;
#endif
  ASSERT( ! slope().null() );
  ASSERT( this->operator()( A ) && this->operator()( B ) );
  ASSERT( before( A, B ) );
  Fraction f10( 1, 0 );
  Pattern<Fraction> p( 0, 1 );
  bool ulu = true;
  bool lul = true;
  Quotient delta = 0;
  Point2I _U = A;
  Point2I _L = A;
  Point2I _Up = _U + Point2I(0,1);
  Point2I _Lp = _L + Point2I(1,-1);
  UnsignedInteger AB1 = (B-A).norm1();
  while ( ( (_Up - A).norm1() <= AB1 )
          && this->operator()( _Up ) ) 
    {
#ifdef TRACE_DSL
      std::cerr << "Vertical" << std::endl;
#endif
     p = Pattern<Fraction>( f10 );
      _Up += Point2I(0,1);
      _Lp += Point2I(0,1);
      ++delta;
    }
  if ( delta != 0 )
    {
      _Lp += Point2I(0,1);
      // ulu = false;
    }
 
  while ( p.slope() != this->slope() )
    {
#ifdef TRACE_DSL
      std::cerr << "[smartDSS] v=" << p.v()
                << " bez=" << p.bezout()
                << " U=(" << _U[0] << "," << _U[1] << ")"
                << " L=(" << _L[0] << "," << _L[1] << ")"
                << " Up=(" << _Up[0] << "," << _Up[1] << ")"
                << " Lp=(" << _Lp[0] << "," << _Lp[1] << ")"
                << std::endl;
#endif
      ASSERT( p.v()[1]*p.bezout()[0] - p.v()[0]*p.bezout()[1] == -1 ); 
      if ( ( (_Up - A).norm1() > AB1 ) &&  ( (_Lp - A).norm1() > AB1 ) ) break;
      else if ( _Up[ 1 ] <= B[ 1 ] && this->operator()( _Up ) )
        {
          Fraction np = p.slope().right();
          for ( Quotient i = 1; i < delta; ++i ) 
            np = np.left();
          _L = _Lp + p.bezout() - p.v();
          if ( ! lul ) _L -= p.v();
          p = Pattern<Fraction>( np );
          ASSERT( p.v()[1]*p.bezout()[0] - p.v()[0]*p.bezout()[1] == -1 ); 
          _Up = _U + p.v() + p.bezout();
          _Lp = _L + p.v() + p.v() - p.bezout();
          delta = 1; ulu = true; lul = false;
        }
      else if ( _Lp[ 0 ] <= B[ 0 ] && this->operator()( _Lp ) )
        {
          Fraction np = p.slope().left();
          for ( Quotient i = 1; i < delta; ++i ) 
            np = np.right();
          _U = p.slope() == f10 ? _Up - Point2I( 0,1 ) : _Up - p.bezout();
          if ( ! ulu ) _U -= p.v();
          p = Pattern<Fraction>( np );
          ASSERT( p.v()[1]*p.bezout()[0] - p.v()[0]*p.bezout()[1] == -1 ); 
          _Up = _U + p.v() + p.bezout();
          _Lp = _L + p.v() + p.v() - p.bezout();
          delta = 1; ulu = false; lul = true;
        }
      else
        {
          ++delta;
          _Up += p.v();
          _Lp += p.v();
        }
    }
  Integer nmu = p.slope().p() * _U[ 0 ] - p.slope().q() * _U[ 1 ];
  return StandardDSLQ0( p.slope(), nmu );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Point DGtal::StandardDSLQ0< TFraction >::U ( ) const

inline

Returns:: the first upper leaning point of the DSL in the first quadrant (x >= 0).

Definition at line 180 of file StandardDSLQ0.ih.

{
  Vector2I u = pattern().bezout();
  Integer c = ( mu() * u[ 0 ] ) / b();
  return Point( mu() > NumberTraits<Integer>::ZERO 
                ? v() * ( c + 1 ) - u * mu()
                : u * mu() - v() * c );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Point DGtal::StandardDSLQ0< TFraction >::uppermostX ( IntegerParamType y ) const

inline

Returns:: the point on this DSL with this y coordinate and uppermost x coordinate.

Definition at line 232 of file StandardDSLQ0.ih.

{
  Integer q = mup() + b() * y;
  return Point( ic.floorDiv( q, a() ), y );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Point DGtal::StandardDSLQ0< TFraction >::uppermostY ( IntegerParamType x ) const

inline

Returns:: the point on this DSL with this x coordinate and uppermost y coordinate.

Definition at line 212 of file StandardDSLQ0.ih.

{
  Integer q = a() * x - mu();
  return Point( x, ic.floorDiv( q, b() ) );
}

template<typename TFraction >

DGtal::StandardDSLQ0< TFraction >::Vector2I DGtal::StandardDSLQ0< TFraction >::v ( ) const

inline

Returns:: the vector for the pattern, ie ( slope().q(), slope().p() )

Definition at line 171 of file StandardDSLQ0.ih.

References DGtal::StandardDSLQ0< TFraction >::v().

Referenced by DGtal::StandardDSLQ0< TFraction >::DSSWithinTwoPatterns(), DGtal::StandardDSLQ0< TFraction >::reversedSmartDSS(), and DGtal::StandardDSLQ0< TFraction >::v().

{
  return pattern().v();
}

Field Documentation

template<typename TFraction>

IC DGtal::StandardDSLQ0< TFraction >::ic

private

Used in some computations.

Definition at line 385 of file StandardDSLQ0.h.

template<typename TFraction>

Integer DGtal::StandardDSLQ0< TFraction >::myMu

protected

the shift to origin.

Definition at line 380 of file StandardDSLQ0.h.

Referenced by DGtal::StandardDSLQ0< TFraction >::operator=().

template<typename TFraction>

Pattern<Fraction> DGtal::StandardDSLQ0< TFraction >::myPattern

protected

the characteristic pattern of this DSL.

Definition at line 378 of file StandardDSLQ0.h.

Referenced by DGtal::StandardDSLQ0< TFraction >::operator=().

The documentation for this class was generated from the following files:

Data Structures

Public Types

Public Member Functions

Protected Attributes

Static Private Member Functions

Private Attributes

Detailed Description

template<typename TFraction> class DGtal::StandardDSLQ0< TFraction >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Field Documentation

template<typename TFraction>
class DGtal::StandardDSLQ0< TFraction >