Warning: MathJax requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

Temporally consistent gradient domain video editing

Gabriele Facciolo, Rida Sadek, Aurelie Bugeau and Vicent Caselles Universitat Pompeu Fabra EMMCVPR 2011
(presentation 26Mb with videos)
Update: Extension to handle brightness changes - webpage.

Abstract

In the context of video editing, enforcing spatio-temporal consistency is an important issue. With that purpose, the current variational models for gradient domain video editing include space and time regularization terms. The spatial terms are based on the usual space derivatives, the temporal ones are based on the convective derivative, and both are balanced by a parameter β. However, the usual discretizations of the convective derivative limit the value of β to a certain range, thus limiting these models from achieving their full potential. In this paper, we propose a new numerical scheme to compute the convective derivative, the deblurring convective derivative, which allows us to lift this constraint. Moreover, the proposed scheme introduces less errors than other discretization schemes without adding computational complexity. We use this scheme in the implementation of two gradient domain models for temporally consistent video editing, based on Poisson and total variation type formulations, respectively. We apply these models to three video editing tasks: inpainting correction, object insertion and object removal.

Description

We consider the following functional for performing gradient domain video editing while enforcing the temporal consistency: \begin{equation} E_{p}(u) = \int_{O\subset \Pi} |\partial_v u(x,t)|^p + \beta \| \nabla_{x} u(x,t) - g(x,t) \|^p \, \mathrm dx\,\mathrm dt . \label{eq:videopoisson} \end{equation}

Video sequence as a
spatio-temporal volume

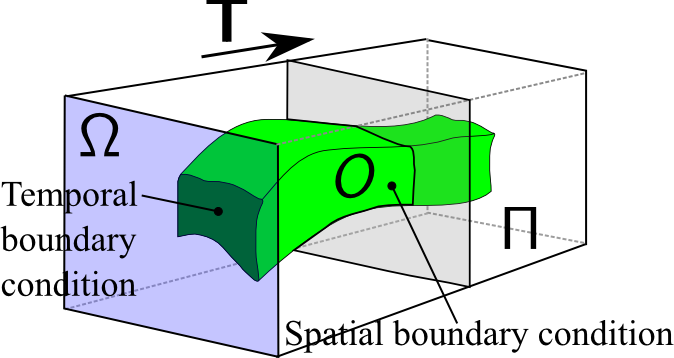
This functional is defined on the spatio-temporal volume $\Pi := \Omega \times \mathbb T$, where $\Omega\subset \mathbb R^2$ is the rectangular image domain, $\mathbb T = [0,T]$ is the temporal domain, and $O\subset \Omega\times \mathbb T$ denotes the spatio-temporal domain where the editing is performed. $u:\Omega\times\mathbb T\rightarrow \mathbb R$ denotes a scalar function representing the video, and $v:\Omega\times\mathbb T\rightarrow \mathbb R^2$ is the velocity field obtained from the unaltered video sequence $u_{0}$. We consider $p\in\{1,2\}$ and $\beta \ge 0$.

The second term is responsible for the gradient domain image editing at each frame, where the field $g:O \rightarrow \mathbb R^2$ is the modified gradient field.
The first term imposes the temporal consistency on the resulting video. Where $\partial_v u(x,t)$ denotes the convective derivative of $u$ along $v$ (a derivative of the video $u$ along the optical flow field $v$).

Discretization of the convective derivative, and the Deblurring Convective Derivative

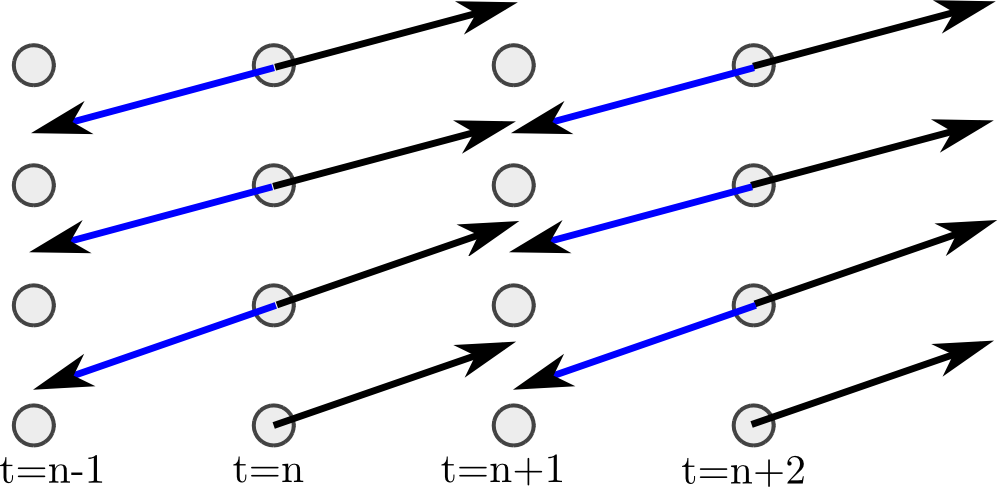
The velocity field $v$ is given by the optical flow of the original video $u_{0}:\Pi\to \mathbb R$. In our experiments we compute it using [Brox et. al. High accuracy optical flow estimation based on a theory for warping. 2004]. The forward optical flow $v^+:\Omega\times \mathbb T\rightarrow \mathbb R^2$ between two frames $u(\cdot, t)$ and $u(\cdot, t+1)$ is the vector field such that $u(x, t)$ and $u(x+v^+(x,t), t+1)$ correspond to the same point in the scene. Similarly, the backward optical flow $v^-$, relates the frame at $t$ with the one at time $t-1$. We can discretize the convective derivative either using the forward or backward optical flow \begin{align} \partial^+_{v}u(x,t) := \hat u(x + v^+(x,t), t+1) -u(x,t), \\ \partial^-_{v}u(x,t) := \hat u(x,t) - u(x + v^-(x,t), t-1) , \end{align} where $\hat u(x + v^+(x,t), t+1)$ is the bilinear interpolation of $u(\cdot, t+1)$ at $x + v^+(x,t)$.

Experiment 1 compares both discretizations of the convective derivative. Observe that the effects of the two discretizations $\partial^-_v$ and $\partial^+_v$ for the convective derivative are somehow opposite. The first introduces blurring in the solution, while the second sharpens the solution and introduces oscillations.

$v^+$- scheme DCD scheme

This observation motivates the search for a new discretization for the convective derivative, one which reduces these distortions end preserve the information for longer periods of time. The idea of the deblurring convective derivative is to attain this objective as the balance of two opposing processes. That is, alternating both schemes to moderate each other's effects.
Expriment 1 shows that it works.

Experiments

In the experiments the blue area indicates the inpainting domain $O$. All the boundary conditions are of Dirichlet type $u\vert_{\partial O \setminus \partial \Pi} = u_{0}$ at ${\partial O \setminus \partial \Pi}$, except for $O \cap \partial \Pi$ where are homogeneous Neuman.

Note: Click on the preview animations for the full videos.