W.J. Cody's approximation of the complementary error function (erfc) More...
Detailed Description
W.J. Cody's approximation of the complementary error function (erfc)
Copyright (c) 2012, Pascal Getreuer All rights reserved.
This program is free software: you can redistribute it and/or modify it under, at your option, the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version, or the terms of the simplified BSD license.
You should have received a copy of these licenses along with this program. If not, see http://www.gnu.org/licenses/ and http://www.opensource.org/licenses/bsd-license.html.
Definition in file erfc_cody.h.
#include <math.h>Go to the source code of this file.
Macros | |
| #define | M_1_SQRTPI 0.564189583547756286948 |
The constant 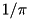 . . | |
| #define | erfc(x) erfc_cody(x) |
| Short alias of erfc_cody() | |
Functions | |
| double | erfc_cody (double x) |
| Complementary error function. More... | |
Function Documentation
| double erfc_cody | ( | double | x | ) |
Complementary error function.
Based on the public domain NETLIB (Fortran) code by W. J. Cody Applied Mathematics Division Argonne National Laboratory Argonne, IL 60439
From the original documentation: The main computation evaluates near-minimax approximations from "Rational Chebyshev approximations for the error function" by W. J. Cody, Math. Comp., 1969, PP. 631-638. This transportable program uses rational functions that theoretically approximate erf(x) and erfc(x) to at least 18 significant decimal digits. The accuracy achieved depends on the arithmetic system, the compiler, the intrinsic functions, and proper selection of the machine-dependent constants.
Definition at line 65 of file erfc_cody.c.
 1.8.3.1
1.8.3.1