Alvarez-Mazorra approximate Gaussian convolution. More...

Detailed Description

Alvarez-Mazorra approximate Gaussian convolution.

Author: Pascal Getreuer getre.nosp@m.uer@.nosp@m.cmla..nosp@m.ens-.nosp@m.cacha.nosp@m.n.fr

This program is free software: you can redistribute it and/or modify it under, at your option, the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version, or the terms of the simplified BSD license.

You should have received a copy of these licenses along with this program. If not, see http://www.gnu.org/licenses/ and http://www.opensource.org/licenses/bsd-license.html.

Definition in file gaussian_conv_am.c.

#include <assert.h>
#include <math.h>
#include "filter_util.h"
#include "gaussian_conv_am.h"

Go to the source code of this file.

Functions
static num	am_left_boundary (const num *data, long N, long stride, num nu, long num_terms)
	Handling of the left boundary for Alvarez-Mazorra. More...

void	am_gaussian_conv (num dest, const num src, long N, long stride, double sigma, int K, num tol, int use_adjusted_q)
	Gaussian convolution with Alvarez-Mazorra. More...

void	am_gaussian_conv_image (num dest, const num src, int width, int height, int num_channels, num sigma, int K, num tol, int use_adjusted_q)
	2D Gaussian convolution with Alvarez-Mazorra More...

Function Documentation

static num am_left_boundary	(	const num *	data,
		long	N,
		long	stride,
		num	nu,
		long	num_terms
	)

static

Handling of the left boundary for Alvarez-Mazorra.

Parameters

data	signal data
N	number of elements
stride	stride between successive samples
nu	filter parameter nu
num_terms	number of terms to use to approximate infinite sum

Returns: the sum approximating the first filtered sample value

This routine approximates the infinite sum 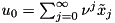$u_0 = \sum_{j=0}^\infty \nu^j \Tilde{x}_j$ by adding the first num_terms terms.

Definition at line 38 of file gaussian_conv_am.c.

Detailed Description

Functions

Function Documentation