#include <SternBrocot.h>

Collaboration diagram for DGtal::SternBrocot< TInteger, TQuotient >::Fraction:

Public Types
typedef TInteger	Integer
typedef TQuotient	Quotient
typedef SternBrocot< TInteger, TQuotient >	SternBrocotTree
typedef SternBrocotTree::Fraction	Self
typedef NumberTraits< Integer > ::UnsignedVersion	UnsignedInteger
typedef std::pair< Quotient, Quotient >	Value
typedef std::vector< Quotient >	CFracSequence
typedef InputIteratorWithRankOnSequence < CFracSequence, Quotient >	ConstIterator
typedef Value	value_type
typedef ConstIterator	const_iterator
typedef const value_type &	const_reference

Public Member Functions
	Fraction (Integer aP, Integer aQ, Fraction ancestor=SternBrocotTree::zeroOverOne())
	Fraction (Node *sb_node=0)
	Fraction (const Self &other)
Self &	operator= (const Self &other)
bool	null () const
Integer	p () const
Integer	q () const
Quotient	u () const
Quotient	k () const
Fraction	left () const
Fraction	right () const
bool	even () const
bool	odd () const
Fraction	father () const
Fraction	father (Quotient m) const
Fraction	previousPartial () const
Fraction	inverse () const
Fraction	partial (Quotient kp) const
Fraction	reduced (Quotient i) const
void	push_back (const std::pair< Quotient, Quotient > &quotient)
void	pushBack (const std::pair< Quotient, Quotient > &quotient)
void	getSplit (Fraction &f1, Fraction &f2) const
void	getSplitBerstel (Fraction &f1, Quotient &nb1, Fraction &f2, Quotient &nb2) const
void	getCFrac (std::vector< Quotient > &quotients) const
bool	equals (Integer p1, Integer q1) const
bool	lessThan (Integer p1, Integer q1) const
bool	moreThan (Integer p1, Integer q1) const
bool	operator== (const Fraction &other) const
bool	operator!= (const Fraction &other) const
bool	operator< (const Fraction &other) const
bool	operator> (const Fraction &other) const
void	selfDisplay (std::ostream &out) const
ConstIterator	begin () const
ConstIterator	end () const

Private Attributes
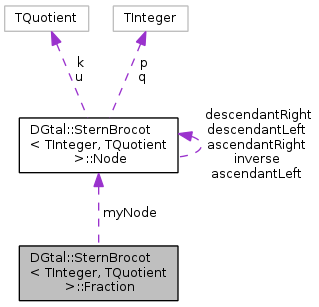
Node *	myNode

Detailed Description

template<typename TInteger, typename TQuotient = int32_t>
class DGtal::SternBrocot< TInteger, TQuotient >::Fraction

This fraction is a model of CPositiveIrreducibleFraction.

It represents a positive irreducible fraction, i.e. some p/q qith gcd(p,q)=1. It is an inner class of SternBrocot. This representation of a fraction is simply a pointer to the corresponding node in this tree.

Definition at line 151 of file SternBrocot.h.

Member Typedef Documentation

template<typename TInteger, typename TQuotient = int32_t>

typedef std::vector<Quotient> DGtal::SternBrocot< TInteger, TQuotient >::Fraction::CFracSequence

Definition at line 159 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef ConstIterator DGtal::SternBrocot< TInteger, TQuotient >::Fraction::const_iterator

Definition at line 164 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef const value_type& DGtal::SternBrocot< TInteger, TQuotient >::Fraction::const_reference

Definition at line 165 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef InputIteratorWithRankOnSequence<CFracSequence,Quotient> DGtal::SternBrocot< TInteger, TQuotient >::Fraction::ConstIterator

Definition at line 160 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef TInteger DGtal::SternBrocot< TInteger, TQuotient >::Fraction::Integer

Definition at line 153 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef TQuotient DGtal::SternBrocot< TInteger, TQuotient >::Fraction::Quotient

Definition at line 154 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef SternBrocotTree::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::Self

Definition at line 156 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef SternBrocot<TInteger,TQuotient> DGtal::SternBrocot< TInteger, TQuotient >::Fraction::SternBrocotTree

Definition at line 155 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef NumberTraits<Integer>::UnsignedVersion DGtal::SternBrocot< TInteger, TQuotient >::Fraction::UnsignedInteger

Definition at line 157 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef std::pair<Quotient, Quotient> DGtal::SternBrocot< TInteger, TQuotient >::Fraction::Value

Definition at line 158 of file SternBrocot.h.

template<typename TInteger, typename TQuotient = int32_t>

typedef Value DGtal::SternBrocot< TInteger, TQuotient >::Fraction::value_type

Definition at line 163 of file SternBrocot.h.

Constructor & Destructor Documentation

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction::Fraction	(	Integer	aP,
		Integer	aQ,
		Fraction	ancestor = `SternBrocotTree::zeroOverOne()`
	)

inline

Any fraction p/q. Complexity is in \( \sum_i u_i \), where u_i are the partial quotients of p/q.

Parameters:

aP	the numerator (>=0)
aQ	the denominator (>=0)
ancestor	(optional) any ancestor of aP/aQ in the tree (for speed-up).

Returns:: the corresponding fraction in the Stern-Brocot tree.

NB: Complexity is bounded by \( 2 \sum_i u_i \), where u_i are the partial quotients of aP/aQ.

Definition at line 70 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::operator=().

{
  this->operator=( SternBrocotTree::fraction( aP, aQ, ancestor ) );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction::Fraction ( Node * sb_node = 0 )

inline

Default constructor.

Parameters:

sb_node the associated node (or 0 for null fraction).

Definition at line 78 of file SternBrocot.ih.

  : myNode( sb_node )
{
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction::Fraction ( const Self & other )

inline

Copy constructor.

Parameters:

other the object to clone.

Definition at line 86 of file SternBrocot.ih.

  : myNode( other.myNode )
{
}

Member Function Documentation

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction::ConstIterator DGtal::SternBrocot< TInteger, TQuotient >::Fraction::begin ( ) const

inline

Returns:: a const iterator pointing on the beginning of the sequence of quotients of this fraction. NB: \( O(\sum_i u_i) \) operation.

Definition at line 483 of file SternBrocot.ih.

{
  CFracSequence* seq = new CFracSequence;
  this->getCFrac( *seq );
  return ConstIterator( seq, seq->begin() );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction::ConstIterator DGtal::SternBrocot< TInteger, TQuotient >::Fraction::end ( ) const

inline

Returns:: a const iterator pointing after the end of the sequence of quotients of this fraction. NB: O(1) operation.

Definition at line 494 of file SternBrocot.ih.

{
  static CFracSequence dummy;
  return ConstIterator( 0, dummy.end() );
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::equals	(	Integer	p1,
		Integer	q1
	)		const

inline

Parameters:

p1	a numerator.
q1	a denominator.

Returns:: 'true' if this is the fraction p1/q1.

Definition at line 155 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::fraction().

{
  return ( this->p() == p1 ) && ( this->q() == q1 );
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::even ( ) const

inline

Returns:: 'true' if it is an even fraction, i.e. its depth k() is even.

Definition at line 266 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left().

{
  return ( k() & 1 ) == 0;
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::father ( ) const

inline

Returns:: the father of this fraction in O(1), ie [u0,...,uk] => [u0,...,uk - 1]

Definition at line 284 of file SternBrocot.ih.

{
  return Fraction( odd() ? myNode->ascendantRight : myNode->ascendantLeft );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::father ( Quotient m ) const

inline

Parameters:

m	a quotient between 1 and uk-1.

Returns:: a given father of this fraction in O(uk - m), ie [u0,...,uk] => [u0,...,m]

Todo:: Do it in O(1)... but require to change the data structure.

Definition at line 293 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantLeft, DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantRight, and DGtal::SternBrocot< TInteger, TQuotient >::Node::u.

{
  if ( m > NumberTraits<Quotient>::ONE ) // > 1
    {
      Node* n = myNode;
      while ( n->u > m )
        n = odd() ? n->ascendantRight : n->ascendantLeft;
      return Fraction( n );
    }
  else if ( m != NumberTraits<Quotient>::ZERO ) // == 1
    {
      return odd() ? previousPartial().right() : previousPartial().left();
    }
  else // == 0
    return reduced( 2 ); //previousPartial().previousPartial();
}

template<typename TInteger , typename TQuotient >

void DGtal::SternBrocot< TInteger, TQuotient >::Fraction::getCFrac ( std::vector< Quotient > & quotients ) const

inline

Parameters:

quotients (returns) the coefficients of the continued fraction of 'this'.

Definition at line 460 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantLeft, DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantRight, DGtal::SternBrocot< TInteger, TQuotient >::Node::k, and DGtal::SternBrocot< TInteger, TQuotient >::Node::u.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::display().

{
  ASSERT( this->k() >= NumberTraits<Quotient>::ZERO );
  int64_t i = NumberTraits<Quotient>::castToInt64_t( this->k() );
  quotients.resize( (unsigned int)i + 1 );
  quotients[ (unsigned int)i-- ] = this->u();
  Node* n = myNode;
  bool bleft = odd() ? true : false;
  while ( i >= 0 )
    {
      ASSERT( n->k >= NumberTraits<Quotient>::ZERO );
      n = bleft ? n->ascendantLeft : n->ascendantRight;
      quotients[ (unsigned int)i ] = 
        ( i == NumberTraits<Quotient>::castToInt64_t( n->k ) ) ? n->u : 1;
      --i;
      bleft = ! bleft;
    }
}

template<typename TInteger , typename TQuotient >

void DGtal::SternBrocot< TInteger, TQuotient >::Fraction::getSplit	(	Fraction &	f1,
		Fraction &	f2
	)		const

inline

Splitting formula, O(1) time complexity. This fraction should not be 0/1 or 1/0. NB: 'this' = [f1] [f2].

Parameters:

f1	(returns) the left part of the split.
f2	(returns) the right part of the split.

Definition at line 427 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantLeft, DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantRight, and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::myNode.

{
  f1.myNode = myNode->ascendantLeft;
  f2.myNode = myNode->ascendantRight;
}

template<typename TInteger , typename TQuotient >

void DGtal::SternBrocot< TInteger, TQuotient >::Fraction::getSplitBerstel	(	Fraction &	f1,
		Quotient &	nb1,
		Fraction &	f2,
		Quotient &	nb2
	)		const

inline

Berstel splitting formula, O(1) time complexity. This fraction should not be 0/1 or 1/0. NB: 'this' = nb1*[f1] nb2*[f2]. Also, if 'this->k' is even then nb1=1, otherwise nb2=1.

Parameters:

f1	(returns) the left part of the split (left pattern).
nb1	(returns) the number of repetition of the left pattern
f2	(returns) the right part of the split (right pattern).
nb2	(returns) the number of repetition of the right pattern

Definition at line 437 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantLeft, DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantRight, and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::myNode.

{
  if ( odd() )
    {
      f1.myNode = myNode->ascendantLeft;
      nb1 = this->u();
      f2.myNode = f1.myNode->ascendantRight;
      nb2 = 1;
    }
  else
    {
      f2.myNode = myNode->ascendantRight;
      nb2 = this->u();
      f1.myNode = f2.myNode->ascendantLeft;
      nb1 = 1;
    }
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::inverse ( ) const

inline

Returns:: the inverse of this fraction in O(1), ie [u0,...,uk] => [0,u0,...,uk] or [0,u0,...,uk] => [u0,...,uk].

Definition at line 326 of file SternBrocot.ih.

{
  return Fraction( myNode->inverse );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Quotient DGtal::SternBrocot< TInteger, TQuotient >::Fraction::k ( ) const

inline

Returns:: its depth (1+number of coefficients of its continued fraction).

Definition at line 145 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::display(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left().

{
  ASSERT( myNode != 0 );
  return myNode->k;
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left ( ) const

inline

Returns:: its left descendant (construct it if it does not exist yet).

Definition at line 220 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::fraction(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::pushBack(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::right().

{
  if ( myNode->descendantLeft == 0 )
    {
      Node* pleft = myNode->ascendantLeft;
      Node* n = new Node( p() + pleft->p, 
                          q() + pleft->q,
                          odd() ? u() + 1 : (Quotient) 2,
                          odd() ? k() : k() + 1,
                          pleft, myNode,
                          0, 0, 0 );
      Fraction inv = Fraction( myNode->inverse );
      Node* invpright = inv.myNode->ascendantRight;
      Node* invn = new Node( inv.p() + invpright->p,
                             inv.q() + invpright->q,
                             inv.even() ? inv.u() + 1 : (Quotient) 2,
                             inv.even() ? inv.k() : inv.k() + 1,
                             myNode->inverse, invpright,
                             0, 0, n );
      n->inverse = invn;
      myNode->inverse->descendantRight = invn;
      myNode->descendantLeft = n;
      instance().nbFractions += 2;
    }
  return Fraction( myNode->descendantLeft );
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::lessThan	(	Integer	p1,
		Integer	q1
	)		const

inline

Parameters:

p1	a numerator.
q1	a denominator.

Returns:: 'true' if this is < to the fraction p/q.

Definition at line 164 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::fraction().

{
  Integer d = p() * q1 - q() * p1;
  return d < NumberTraits<Integer>::ZERO;
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::moreThan	(	Integer	p1,
		Integer	q1
	)		const

inline

Parameters:

p1	a numerator.
q1	a denominator.

Returns:: 'true' if this is > to the fraction p1/q1.

Definition at line 174 of file SternBrocot.ih.

{
  Integer d = p() * q1 - q() * p1;
  return d > NumberTraits<Integer>::ZERO;
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::null ( ) const

inline

Returns:: 'true' iff it is the null fraction 0/0.

Definition at line 108 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::display().

{
  return myNode == 0;
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::odd ( ) const

inline

Returns:: 'true' if it is an odd fraction, i.e. its depth k() is odd.

Definition at line 275 of file SternBrocot.ih.

{
  return ( k() & 1 ) != 0;
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator!= ( const Fraction & other ) const

inline

Parameters:

other any fraction.

Returns:: 'true' iff this is different from other.

Definition at line 193 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Fraction::myNode.

{
  return myNode != other.myNode;
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator< ( const Fraction & other ) const

inline

Parameters:

other any fraction.

Returns:: 'true' iff this is < to other.

Definition at line 202 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Fraction::p(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::q().

{
  return this->lessThan( other.p(), other.q() );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction & DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator= ( const Self & other )

inline

Assignment

Parameters:

other the object to clone.

Returns:: a reference to 'this'.

Definition at line 95 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Fraction::myNode.

{
  if ( this != &other )
    {
      myNode = other.myNode;
    }
  return *this;
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator== ( const Fraction & other ) const

inline

Parameters:

other any fraction.

Returns:: 'true' iff this is equal to other.

Definition at line 184 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Fraction::myNode.

{
  return myNode == other.myNode;
}

template<typename TInteger , typename TQuotient >

bool DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator> ( const Fraction & other ) const

inline

Parameters:

other any fraction.

Returns:: 'true' iff this is > to other.

Definition at line 211 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Fraction::p(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::q().

{
  return this->moreThan( other.p(), other.q() );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Integer DGtal::SternBrocot< TInteger, TQuotient >::Fraction::p ( ) const

inline

Returns:: its numerator;

Definition at line 117 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::display(), DGtal::SternBrocot< TInteger, TQuotient >::fraction(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator<(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator>().

{
  return myNode ? myNode->p : 0;
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::partial ( Quotient kp ) const

inline

Parameters:

kp	the chosen depth of the partial fraction (kp <= k()).

Returns:: the partial fraction of depth kp, ie. [u0,...,uk] => [u0,...,ukp]

Definition at line 335 of file SternBrocot.ih.

{
  ASSERT( ( ((Quotient)-2) <= kp ) && ( kp <= k() ) );
  return reduced( k() - kp );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::previousPartial ( ) const

inline

Returns:: the previous partial of this fraction in O(1), ie [u0,...,u{k-1},uk] => [u0,...,u{k-1}]. Otherwise said, it is its ascendant with a smaller depth.

Definition at line 314 of file SternBrocot.ih.

{
  return Fraction( odd() ? myNode->ascendantLeft : myNode->ascendantRight );
  // return Fraction( odd() 
  //                 ? myNode->ascendantLeft->descendantRight
  //                 : myNode->ascendantRight->descendantLeft );
}

template<typename TInteger , typename TQuotient >

void DGtal::SternBrocot< TInteger, TQuotient >::Fraction::push_back ( const std::pair< Quotient, Quotient > & quotient )

inline

    Modifies this fraction \form#77 to obtain the
    fraction \form#147. The depth of the quotient
    must be given, since continued fractions have two writings

\([u_0,...,u_k]\) and \([u_0,...,u_k - 1, 1]\).

    Useful to create output iterators, for instance with

    @code 
    typedef ... Fraction; 
    Fraction f;
    std::back_insert_iterator<Fraction> itout = std::back_inserter( f );
    @endcode

    @param quotient the pair \form#76.

Definition at line 364 of file SternBrocot.ih.

{
  pushBack( quotient );
}

template<typename TInteger , typename TQuotient >

void DGtal::SternBrocot< TInteger, TQuotient >::Fraction::pushBack ( const std::pair< Quotient, Quotient > & quotient )

inline

    Modifies this fraction \form#77 to obtain the
    fraction \form#147. The depth of the quotient
    must be given, since continued fractions have two writings

\([u_0,...,u_k]\) and \([u_0,...,u_k - 1, 1]\).

    See push_back for creating output iterators.

    @param quotient the pair \form#76.

Definition at line 373 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left(), DGtal::SternBrocot< TInteger, TQuotient >::oneOverZero(), DGtal::SternBrocot< TInteger, TQuotient >::operator=(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::right(), and DGtal::SternBrocot< TInteger, TQuotient >::zeroOverOne().

{
  // std::vector<Quotient> quots;
  // if ( ! null() )
  //   {
  //     this->getCFrac( quots );
  //     std::cerr << "F[";
  //     for ( unsigned int i = 0; i < quots.size(); ++i )
  //       std::cerr << " " << quots[ i ];
  //   }
  // else std::cerr << "[";
  // std::cerr << "] + " << "(" << quotient.first 
  //           << "," << quotient.second << ")";
  if ( null() )
    {
      ASSERT( quotient.second <= NumberTraits<Quotient>::ZERO );
      if ( quotient.second < NumberTraits<Quotient>::ZERO )
        this->operator=( oneOverZero() );
      else if ( quotient.first == NumberTraits<Quotient>::ZERO ) // (0,0)
        this->operator=( zeroOverOne() );
      else
        {
          Fraction f = zeroOverOne();
          for ( Quotient i = 0; i < quotient.first; ++i )
            f = f.right();
          this->operator=( f );
        }
    }
  else if ( NumberTraits<Quotient>::even( quotient.second ) )
    {
      Fraction f = left();
      for ( Quotient i = 1; i < quotient.first; ++i )
        f = f.right();
      this->operator=( f );
    }
  else
    {
      Fraction f = right();
      for ( Quotient i = 1; i < quotient.first; ++i )
        f = f.left();
      this->operator=( f );
    }
  // quots.clear();
  // this->getCFrac( quots );
  // std::cerr << " => F[";
  // for ( unsigned int i = 0; i < quots.size(); ++i )
  //   std::cerr << " " << quots[ i ];
  // std::cerr << "]" << std::endl;
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Integer DGtal::SternBrocot< TInteger, TQuotient >::Fraction::q ( ) const

inline

Returns:: its denominator;

Definition at line 126 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::display(), DGtal::SternBrocot< TInteger, TQuotient >::fraction(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator<(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator>().

{
  return myNode ? myNode->q : 0;
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::reduced ( Quotient i ) const

inline

Parameters:

i	a positive integer smaller or equal to k()+2.

Returns:: the partial fraction of depth k()-i, ie. [u0,...,uk] => [u0,...,u{k-i}]

Definition at line 345 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantLeft, DGtal::SternBrocot< TInteger, TQuotient >::Node::ascendantRight, and DGtal::SternBrocot< TInteger, TQuotient >::Node::k.

{
  ASSERT( ( ((Quotient)0) <= i ) && ( i <= ( k()+((Quotient)2) ) ) );
  Node* n = this->myNode;
  bool bleft = ( n->k & NumberTraits<Quotient>::ONE ) 
    != NumberTraits<Quotient>::ZERO;
  while ( i-- > NumberTraits<Quotient>::ZERO )
    {
      n = bleft ? n->ascendantLeft : n->ascendantRight;
      bleft = ! bleft;
    }
  return Fraction( n );
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Fraction DGtal::SternBrocot< TInteger, TQuotient >::Fraction::right ( ) const

inline

Returns:: its right descendant (construct it if it does not exist yet).

Definition at line 251 of file SternBrocot.ih.

References DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left().

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::fraction(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::pushBack().

{
  if ( myNode->descendantRight == 0 )
    {
      Fraction inv( myNode->inverse );
      inv.left();
      ASSERT( myNode->descendantRight !=  0 );
    }
  return Fraction( myNode->descendantRight );
}

template<typename TInteger , typename TQuotient >

void DGtal::SternBrocot< TInteger, TQuotient >::Fraction::selfDisplay ( std::ostream & out ) const

inline

Writes/Displays the fraction on an output stream.

Parameters:

out	the output stream where the object is written.

Definition at line 504 of file SternBrocot.ih.

{
  if ( this->null() ) out << "[Fraction null]";
  else
    {
      out << "[Fraction f=" << this->p() 
          << "/" << this->q()
          << " u=" << this->u()
          << " k=" << this->k()
          << std::flush;
      std::vector<Quotient> quotients;
      if ( this->k() >= 0 )
        {
          this->getCFrac( quotients );
          out << " [" << quotients[ 0 ];
          for ( unsigned int i = 1; i < quotients.size(); ++i )
            out << "," << quotients[ i ];
          out << "]";
        }
      out << " ]";
    }
}

template<typename TInteger , typename TQuotient >

DGtal::SternBrocot< TInteger, TQuotient >::Quotient DGtal::SternBrocot< TInteger, TQuotient >::Fraction::u ( ) const

inline

Returns:: its quotient (last coefficient of its continued fraction).

Definition at line 135 of file SternBrocot.ih.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::display(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left().

{
  ASSERT( myNode != 0 );
  return myNode->u;
}

Field Documentation

template<typename TInteger, typename TQuotient = int32_t>

Node* DGtal::SternBrocot< TInteger, TQuotient >::Fraction::myNode

private

Definition at line 168 of file SternBrocot.h.

Referenced by DGtal::SternBrocot< TInteger, TQuotient >::Fraction::getSplit(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::getSplitBerstel(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::left(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator!=(), DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator=(), and DGtal::SternBrocot< TInteger, TQuotient >::Fraction::operator==().

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Private Attributes

Detailed Description

template<typename TInteger, typename TQuotient = int32_t> class DGtal::SternBrocot< TInteger, TQuotient >::Fraction

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Field Documentation

template<typename TInteger, typename TQuotient = int32_t>
class DGtal::SternBrocot< TInteger, TQuotient >::Fraction