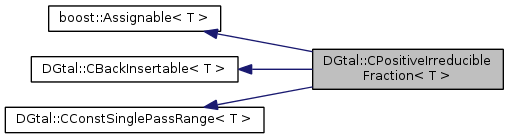
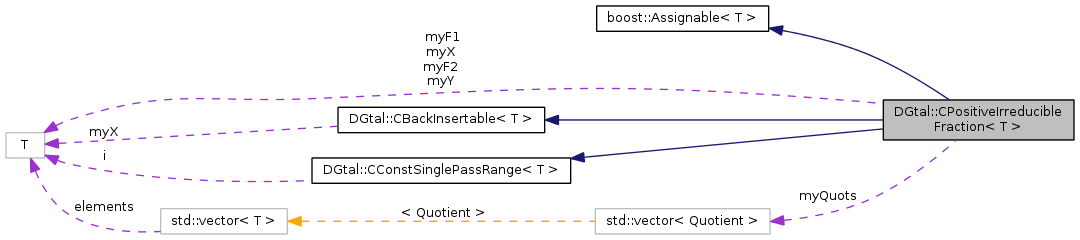
#include <CPositiveIrreducibleFraction.h>

Inheritance diagram for DGtal::CPositiveIrreducibleFraction< T >:

Collaboration diagram for DGtal::CPositiveIrreducibleFraction< T >:

Public Types
typedef T::Integer	Integer
typedef T::Quotient	Quotient
typedef T::value_type	value_type
typedef T::Value	Value
typedef T::ConstIterator	ConstIterator
typedef T::const_iterator	const_iterator
Public Types inherited from DGtal::CBackInsertable< T >
Public Types inherited from DGtal::CConstSinglePassRange< T >

Public Member Functions
	BOOST_CONCEPT_ASSERT ((CInteger< Integer >))
	BOOST_CONCEPT_ASSERT ((CSignedInteger< Quotient >))
	BOOST_STATIC_ASSERT ((ConceptUtils::SameType< value_type, std::pair< Quotient, Quotient > >::value))
	BOOST_STATIC_ASSERT ((ConceptUtils::SameType< value_type, Value >::value))
	BOOST_CONCEPT_USAGE (CPositiveIrreducibleFraction)
void	checkConstConstraints () const
Public Member Functions inherited from DGtal::CBackInsertable< T >
	BOOST_CONCEPT_USAGE (CBackInsertable)
Public Member Functions inherited from DGtal::CConstSinglePassRange< T >
	BOOST_CONCEPT_ASSERT ((boost_concepts::SinglePassIteratorConcept< ConstIterator >))
	BOOST_CONCEPT_USAGE (CConstSinglePassRange)

Private Attributes
T	myX
T	myY
Integer	myP
Integer	myQ
Quotient	myU
bool	myBool
Quotient	myN1
Quotient	myN2
T	myF1
T	myF2
std::vector< Quotient >	myQuots
std::pair< Quotient, Quotient >	myValue
ConstIterator	myIterator

Detailed Description

template<typename T>
struct DGtal::CPositiveIrreducibleFraction< T >

Aim: Defines positive irreducible fractions, i.e. fraction p/q, p and q non-negative integers, with gcd(p,q)=1.

Description of concept 'CPositiveIrreducibleFraction'

Irreducible fractions are nicely represented with the Stern-Brocot tree. Furthermore, the development of a fraction p/q into its simple continued fraction with quotients \([u_0, \ldots, u_k]\) has one-to-one correspondence with the position of the fraction in the Stern-Brocot tree.

One can "visit" irreducible fractions by enumerating the sequence of its partial quotients. Furthermore, one can push a new quotient at the end of this fraction to get a new fraction which shares all quotients except the last one. In this sense, a fraction is a sequence (container) that can only grow.

Refinement of

boost::CopyConstructible, boost::DefaultConstructible, boost::Assignable
CBackInsertable, CConstSinglePassRange

Associated types :

Integer: the type for representing a numerator or a denominator. Must be a model of CInteger.

Quotient: the type for representing partial quotients, i.e. the integers that appear in the continued fractions of p/q, and for representing the depth of the fraction. Might be the same as Integer but may be also smaller, since quotients are generally much smaller than the convergent numerators and denominators. Must be a model of CSignedInteger since depths may be negative (1/0 is -1).

Value and value_type: the type std::pair<Quotient,Quotient>, useful to create back insertion sequence.

ConstIterator const_iterator: the type for visiting the quotients of the fraction in sequence. The value of the iterator has type Value.

Notation

X : A type that is a model of CPositiveIrreducibleFraction
x : object of type X, which is below some fraction written \([u_0, \ldots, u_k]\) as a continued fraction
x1, x2, y : other objects of type X
p, q : object of type Integer
m, n1, n2 : objects of type Quotient
quots : an object of type std::vector<Quotient>
pair : a object of std::pair<Quotient,Quotient>, here (m,k+1)

Definitions

Valid expressions and semantics

Name	Expression	Return type	Precondition	Semantics	Complexity
Constructor	`Fraction`( p, q )	X		creates the fraction p'/q', where p'=p/g, q'=q/g, g=gcd(p,q)	o(p+q)
numerator	x.`p()`	Integer	! x.`null()`	returns the numerator	O(1)
denominator	x.`q()`	Integer	! x.`null()`	returns the denominator	O(1)
quotient	x.`u()`	Quotient	! x.`null()`	returns the quotient \(u_k\)	O(1)
depth	x.`k()`	Quotient	! x.`null()`	returns the depth k	O(1)
null test	x.`null()`	`bool`		returns 'true' if the fraction is null 0/0 (default fraction)	O(1)
even parity	x.`even()`	`bool`	! x.`null()`	returns 'true' iff the fraction is even, i.e. k is even	O(1)
odd parity	x.`odd()`	`bool`	! x.`null()`	returns 'true' iff the fraction is odd, i.e. k is odd	O(1)

left descendant	x.`left()`	X	! x.`null()`	returns the left descendant of p/q in the Stern-Brocot tree	O(1)
right descendant	x.`right()`	X	! x.`null()`	returns the right descendant of p/q in the Stern-Brocot tree	O(1)
father	x.`father()`	X	! x.`null()`	returns the father of this fraction, ie \([u_0,...,u_k - 1]\)	O(1)
m-father	x.`father`(m)	X	! x.`null()`, m>=0	returns the m-father of this fraction, ie \([u_0,...,u_{k-1}, m]\)	O( m)
previousPartial	x.`previousPartial()`	X	! x.`null()`	returns the previous partial of this fraction, ie \([u_0,...,u_{k-1}]\)	O(1)
inverse	x.`inverse()`	X	! x.`null()`	returns the inverse of this fraction, ie \([0,u_0,...,u_k]\) if \(u_0 \neq 0 \) or \([u_1,...,u_k]\) otherwise	O(1)
m-th partial	x.`partial(m)`	X	! x.`null()`	returns the m-th partial of this fraction, ie \([u_0,...,u_m]\)	O(1)
m-th reduced	x.`reduced(m)`	X	! x.`null()`	returns the m-th reduced of this fraction, equivalently the \(k-m\) partial, ie \([u_0,...,u_{k-m}]\)	O(1)
splitting formula	x.`getSplit`(x1, x2)	`void`	! x.`null()`	modifies fractions x1 and x2 such that \( x1 \oplus x2 = x \)	O(1)
Berstel splitting formula	x.`getSplitBerstel`(x1, n1, x2, n2)	`void`	! x.`null()`	modifies fractions x1 and x2 and integers n1 and n2 such that \( (x1)^{n1} \oplus (x2)^{n2} = x \)	O(1)
Continued fraction coefficients	x.`getCFrac`(quots)	`void`		modifies the vector quots such that it contains the quotients \(u_0,u_1,...,u_k \)	O(k)

equality	x.`equals`(p, q)	`bool`		returns 'true' iff the fraction is equal to \( p / q \).	O(1)
less than	x.`lessThan`(p, q)	`bool`		returns 'true' iff the fraction is inferior to \( p / q \).	O(1)
more than	x.`moreThan`(p, q)	`bool`		returns 'true' iff the fraction is superior to \( p / q \).	O(1)
equality ==	x == y	`bool`		returns 'true' iff the fraction is equal to y.	O(1)
inequality !=	x != y	`bool`		returns 'true' iff the fraction is different from y.	O(1)
less than <	x < y	`bool`		returns 'true' iff the fraction is inferior to y.	O(1)
more than >	x > y	`bool`		returns 'true' iff the fraction is superior to y.	O(1)

Next continued fraction	x.pushBack( pair )			transforms this fraction \([0,u_0,...,u_k]\) into \([0,u_0,...,u_k,m]\), where pair is \((m,k+1)\)	O(m)
Next continued fraction	x.push_back( pair )			transforms this fraction \([0,u_0,...,u_k]\) into \([0,u_0,...,u_k,m]\), where pair is \((m,k+1)\)	O(m)

Begin visiting quotients	x.begin()	ConstIterator		returns a forward iterator on the beginning of the sequence of quotients \([u_0,...,u_k]\)
End visiting quotients	x.end()	ConstIterator		returns a forward iterator after the end of the sequence of quotients \([u_0,...,u_k]\)

Invariants

Models

SternBrocot::Fraction, LighterSternBrocot::Fraction
also LightSternBrocot::Fraction (but do not use).

Notes

Template Parameters:

T	the type that should be a model of CPositiveIrreducibleFraction.

Definition at line 160 of file CPositiveIrreducibleFraction.h.

Member Typedef Documentation

template<typename T >

typedef T::const_iterator DGtal::CPositiveIrreducibleFraction< T >::const_iterator

Definition at line 171 of file CPositiveIrreducibleFraction.h.

template<typename T >

typedef T::ConstIterator DGtal::CPositiveIrreducibleFraction< T >::ConstIterator

Reimplemented from DGtal::CConstSinglePassRange< T >.

Definition at line 170 of file CPositiveIrreducibleFraction.h.

template<typename T >

typedef T::Integer DGtal::CPositiveIrreducibleFraction< T >::Integer

Definition at line 166 of file CPositiveIrreducibleFraction.h.

template<typename T >

typedef T::Quotient DGtal::CPositiveIrreducibleFraction< T >::Quotient

Definition at line 167 of file CPositiveIrreducibleFraction.h.

template<typename T >

typedef T::Value DGtal::CPositiveIrreducibleFraction< T >::Value

Definition at line 169 of file CPositiveIrreducibleFraction.h.

template<typename T >

typedef T::value_type DGtal::CPositiveIrreducibleFraction< T >::value_type

Reimplemented from DGtal::CBackInsertable< T >.

Definition at line 168 of file CPositiveIrreducibleFraction.h.

Member Function Documentation

template<typename T >

DGtal::CPositiveIrreducibleFraction< T >::BOOST_CONCEPT_ASSERT ( (CInteger< Integer >) )

template<typename T >

DGtal::CPositiveIrreducibleFraction< T >::BOOST_CONCEPT_ASSERT ( (CSignedInteger< Quotient >) )

template<typename T >

DGtal::CPositiveIrreducibleFraction< T >::BOOST_CONCEPT_USAGE ( CPositiveIrreducibleFraction< T > )

inline

Definition at line 178 of file CPositiveIrreducibleFraction.h.

References DGtal::CPositiveIrreducibleFraction< T >::checkConstConstraints(), DGtal::CPositiveIrreducibleFraction< T >::myP, DGtal::CPositiveIrreducibleFraction< T >::myQ, DGtal::CPositiveIrreducibleFraction< T >::myValue, DGtal::CPositiveIrreducibleFraction< T >::myX, and DGtal::ConceptUtils::sameType().

  {
    ConceptUtils::sameType( myX, T( myP, myQ ) );
    myX.push_back( myValue );
    myX.pushBack( myValue );
    checkConstConstraints();
  }

template<typename T >

DGtal::CPositiveIrreducibleFraction< T >::BOOST_STATIC_ASSERT ( (ConceptUtils::SameType< value_type, std::pair< Quotient, Quotient > >::value) )

template<typename T >

DGtal::CPositiveIrreducibleFraction< T >::BOOST_STATIC_ASSERT ( (ConceptUtils::SameType< value_type, Value >::value) )

template<typename T >

void DGtal::CPositiveIrreducibleFraction< T >::checkConstConstraints ( ) const

inline

Reimplemented from DGtal::CBackInsertable< T >.

Definition at line 185 of file CPositiveIrreducibleFraction.h.

Referenced by DGtal::CPositiveIrreducibleFraction< T >::BOOST_CONCEPT_USAGE().

  {
    ConceptUtils::sameType( myP, myX.p() );
    ConceptUtils::sameType( myQ, myX.q() );
    ConceptUtils::sameType( myU, myX.u() );
    ConceptUtils::sameType( myU, myX.k() );
    ConceptUtils::sameType( myBool, myX.null() );
    ConceptUtils::sameType( myX, myX.left() );
    ConceptUtils::sameType( myX, myX.right() );
    ConceptUtils::sameType( myBool, myX.even() );
    ConceptUtils::sameType( myBool, myX.odd() );
    ConceptUtils::sameType( myX, myX.father() );
    ConceptUtils::sameType( myX, myX.father( myU ) );
    ConceptUtils::sameType( myX, myX.previousPartial() );
    ConceptUtils::sameType( myX, myX.inverse() );
    ConceptUtils::sameType( myX, myX.partial( myU ) );
    ConceptUtils::sameType( myX, myX.reduced( myU ) );
    myX.getSplit( myF1, myF2 );
    myX.getSplitBerstel( myF1, myN1, myF2, myN2 );
    myX.getCFrac( myQuots );
    ConceptUtils::sameType( myBool, myX.equals( myP, myQ ) );
    ConceptUtils::sameType( myBool, myX.lessThan( myP, myQ ) );
    ConceptUtils::sameType( myBool, myX.moreThan( myP, myQ ) );
    ConceptUtils::sameType( myBool, myX == myY );
    ConceptUtils::sameType( myBool, myX != myY );
    ConceptUtils::sameType( myBool, myX < myY );
    ConceptUtils::sameType( myBool, myX > myY );
    ConceptUtils::sameType( myIterator, myX.begin() );
    ConceptUtils::sameType( myIterator, myX.end() );
  }