An accurate recursive filter approximation, computed out-of-place. More...

Detailed Description

An accurate recursive filter approximation, computed out-of-place.

Deriche uses a sum of causal and an anticausal recursive filters to approximate the Gaussian. The causal filter has the form

$H^{(K)}(z) = \frac{1}{\sqrt{2\pi\sigma^2}}\sum_{k=1}^K \frac{\alpha_k} {1-\mathrm{e}^{-\lambda_k/\sigma} z^{-1}} = \frac{\sum_{k=0}^{K-1}b_k z^{-k}}{1+\sum_{k=1}^{K}a_k z^{-k}},$

where K is the filter order (2, 3, or 4). The anticausal form is the spatial reversal of the causal filter minus the sample at n = 0, 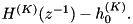$H^{(K)}(z^{-1}) - h_0^{(K)}.$

The process to use these functions is the following:

deriche_precomp() to precompute coefficients for the convolution
deriche_gaussian_conv() or deriche_gaussian_conv_image() to perform the convolution itself (may be called multiple times if desired)

Example: deriche_coeffs c;

num *buffer;

deriche_precomp(&c, sigma, K, tol);

buffer = (num *)malloc(sizeof(num) * 2 * N);

deriche_gaussian_conv(c, dest, buffer, src, N, stride);

free(buffer);

Note: When the num typedef is set to single-precision arithmetic, deriche_gaussian_conv() may be inaccurate for large values of sigma.

Reference

R. Deriche, "Recursively Implementing the Gaussian and its Derivatives," INRIA Research Report 1893, France, 1993. http://hal.inria.fr/docs/00/07/47/78/PDF/RR-1893.pdf

Data Structures
struct	deriche_coeffs
	Coefficients for Deriche Gaussian approximation. More...

Macros
#define	DERICHE_MIN_K 2
	Minimum Deriche filter order.

#define	DERICHE_MAX_K 4
	Maximum Deriche filter order.

#define	DERICHE_VALID_K(K) (DERICHE_MIN_K <= (K) && (K) <= DERICHE_MAX_K)
	Test whether a given K value is a valid Deriche filter order.

Typedefs
typedef struct deriche_coeffs	deriche_coeffs
	Coefficients for Deriche Gaussian approximation. More...

Functions
static void	make_filter (num result_b, num result_a, const complex alpha, const complex beta, int K, double sigma)
	Make Deriche filter from alpha and beta coefficients. More...

void	deriche_precomp (deriche_coeffs *c, double sigma, int K, num tol)
	Precompute coefficients for Deriche's Gaussian approximation. More...

void	deriche_gaussian_conv (deriche_coeffs c, num dest, num buffer, const num *src, long N, long stride)
	Deriche Gaussian convolution. More...

void	deriche_gaussian_conv_image (deriche_coeffs c, num dest, num buffer, const num *src, int width, int height, int num_channels)
	Deriche Gaussian 2D convolution. More...

Typedef Documentation

typedef struct deriche_coeffs deriche_coeffs

Coefficients for Deriche Gaussian approximation.

The deriche_coeffs struct stores the filter coefficients for the causal and anticausal recursive filters of order K. This struct allows to precompute these filter coefficients separately from actually performing the filtering so that filtering may be performed multiple times using the same precomputed coefficients.

This coefficients struct is precomputed by deriche_precomp() and then used by deriche_gaussian_conv() or deriche_gaussian_conv_image().

Function Documentation

void deriche_gaussian_conv	(	deriche_coeffs	c,
		num *	dest,
		num *	buffer,
		const num *	src,
		long	N,
		long	stride
	)

Deriche Gaussian convolution.

Parameters

c	coefficients precomputed by deriche_precomp()
dest	output convolved data
buffer	workspace array with space for at least 2 * N elements
src	input, overwritten if src = dest
N	number of samples
stride	stride between successive samples

This routine performs Deriche's recursive filtering approximation of Gaussian convolution. The Gaussian is approximated by summing the responses of a causal filter and an anticausal filter. The causal filter has the form

$H^{(K)}(z) = \frac{\sum_{k=0}^{K-1} b^+_k z^{-k}} {1 + \sum_{k=1}^K a_k z^{-k}},$

where K is the filter order (2, 3, or 4). The anticausal form is the spatial reversal of the causal filter minus the sample at n = 0, 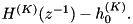$H^{(K)}(z^{-1}) - h_0^{(K)}.$

The filter coefficients 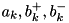$ a_k, b^+_k, b^-_k $ correspond to the variables c.a, c.b_causal, and c.b_anticausal, which are precomputed by the routine deriche_precomp().

The convolution can be performed in-place by setting src = dest (the source array is overwritten with the result). However, the buffer array must be distinct from src.

Note: When the num typedef is set to single-precision arithmetic, results may be inaccurate for large values of sigma.

Definition at line 211 of file gaussian_conv_deriche.c.

void deriche_gaussian_conv_image	(	deriche_coeffs	c,
		num *	dest,
		num *	buffer,
		const num *	src,
		int	width,
		int	height,
		int	num_channels
	)

Deriche Gaussian 2D convolution.

Parameters

c	coefficients precomputed by deriche_precomp()
dest	output convolved data
buffer	array with at least 2*max(width,height) elements
src	input image, overwritten if src = dest
width	image width
height	image height
num_channels	number of image channels

Similar to deriche_gaussian_conv(), this routine approximates 2D Gaussian convolution with Deriche recursive filtering.

The convolution can be performed in-place by setting src = dest (the source array is overwritten with the result). However, the buffer array must be distinct from src.

Note: When the num typedef is set to single-precision arithmetic, results may be inaccurate for large values of sigma.

Definition at line 347 of file gaussian_conv_deriche.c.

void deriche_precomp	(	deriche_coeffs *	c,
		double	sigma,
		int	K,
		num	tol
	)

Precompute coefficients for Deriche's Gaussian approximation.

Parameters

c	deriche_coeffs pointer to hold precomputed coefficients
sigma	Gaussian standard deviation
K	filter order = 2, 3, or 4
tol	accuracy for filter initialization at the boundaries

This routine precomputes the recursive filter coefficients for Deriche's Gaussian convolution approximation. The recursive filters are created through the following steps:

First, the causal filter is represented in the form
$H^{(K)}(z) = \frac{1}{\sqrt{2\pi\sigma^2}}\sum_{k=1}^K \frac{\alpha_k} {1 - \mathrm{e}^{-\lambda_k/\sigma} z^{-1}},$
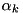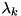where the $\alpha_k$ and $\lambda_k$ are Deriche's optimized parameters and 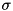$\sigma$ is the specified sigma value.
Setting 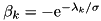$\beta_k = -\mathrm{e}^{-\lambda_k/\sigma}$ , the filter is algebraically rearranged by make_filter() to the form
$\frac{1}{\sqrt{2\pi\sigma^2}}\sum_{k=0}^{K-1}\frac{\alpha_k}{1+\beta_k z^{-1}}=\frac{\sum_{k=0}^{K-1}b_k z^{-k}}{1+\sum_{k=1}^{K}a_k z^{-k}}$
to obtain the numerator and denominator coefficients for the causal filter.
The anticausal filter is determined according to
$\frac{\sum_{k=1}^K b^-_k z^k}{1+\sum_{k=1}^K a_k z^k}= H^{(K)}(z^{-1})- h_0^{(K)}=\frac{\sum_{k=1}^K(b^+_k-a_k b^+_0)z^k}{1+\sum_{k=1}^K a_k z^k}.$

Definition at line 62 of file gaussian_conv_deriche.c.

static void make_filter	(	num *	result_b,
		num *	result_a,
		const complex *	alpha,
		const complex *	beta,
		int	K,
		double	sigma
	)

static

Make Deriche filter from alpha and beta coefficients.

Parameters

result_b	resulting numerator filter coefficients
result_a	resulting denominator filter coefficients
alpha,beta	input coefficients
K	number of terms
sigma	Gaussian sigma parameter

This routine performs the algebraic rearrangement

$\frac{1}{\sqrt{2\pi\sigma^2}}\sum_{k=0}^{K-1}\frac{\alpha_k}{1+\beta_k z^{-1}}=\frac{\sum_{k=0}^{K-1}b_k z^{-k}}{1+\sum_{k=1}^{K}a_k z^{-k}}$

to obtain the numerator and denominator coefficients for the causal filter in Deriche's Gaussian approximation.

The routine initializes b/a as the 0th term,

$\frac{b(z)}{a(z)} = \frac{\alpha_0}{1 + \beta_0 z^{-1}},$

then the kth term is added according to

$\frac{b(z)}{a(z)}\leftarrow\frac{b(z)}{a(z)}+\frac{\alpha_k}{1+\beta_k z^{-1}}=\frac{b(z)(1+\beta_kz^{-1})+a(z)\alpha_k}{a(z)(1+\beta_kz^{-1})}.$

Definition at line 145 of file gaussian_conv_deriche.c.

Detailed Description

Data Structures

Macros

Typedefs

Functions

Typedef Documentation

Function Documentation