Approximation by finite impulse response filtering. More...

Detailed Description

Approximation by finite impulse response filtering.

This code approximates Gaussian convolution with finite impulse response (FIR) filtering. By truncating the Gaussian to a finite support, Gaussian convolution is approximated by

$H(z) = \tfrac{1}{s(r)}\sum_{n=-r}^r G_\sigma(n) z^{-n}, \quad s(r) = \sum_{n=-r}^{r} G_\sigma(n).$

The process to use these functions is the following:

fir_precomp() to precompute filter coefficients for the convolution
fir_gaussian_conv() or fir_gaussian_conv_image() to perform the convolution itself (may be called multiple times if desired)
fir_free() to clean up

Example: fir_coeffs c;

fir_precomp(&c, sigma, tol);

fir_gaussian_conv(c, dest, src, N, stride);

fir_free(&c);

Data Structures
struct	fir_coeffs_
	Coefficients for FIR Gaussian approximation. More...

Typedefs
typedef struct fir_coeffs_	fir_coeffs
	Coefficients for FIR Gaussian approximation.

Functions
static num *	make_g_trunc (num sigma, long r)
	Construct truncated Gaussian filter for FIR convolution. More...

static void	conv_sym (num dest, const num src, long N, long stride, const num *h, long r)
	Convolution with a symmetric filter. More...

int	fir_precomp (fir_coeffs *c, double sigma, num tol)
	Precompute filter coefficients for FIR filtering. More...

void	fir_gaussian_conv (fir_coeffs c, num dest, const num src, long N, long stride)
	FIR Gaussian convolution. More...

void	fir_gaussian_conv_image (fir_coeffs c, num dest, num buffer, const num *src, int width, int height, int num_channels)
	FIR filtering approximation of 2D Gaussian convolution. More...

void	fir_free (fir_coeffs *c)
	Release memory associated with fir_coeffs struct. More...

Function Documentation

static void conv_sym	(	num *	dest,
		const num *	src,
		long	N,
		long	stride,
		const num *	h,
		long	r
	)

static

Convolution with a symmetric filter.

Parameters

dest	destination (must be distinct from src)
src	source signal
N	signal length
stride	stride between successive src and dest samples
h	symmetric filter, an array of length r + 1
r	radius of filter h

This routine computes the convolution of src and h according to

$\mathrm{dest[stride*n]} = \sum_{|m| \le r} h_{|m|} \, \mathrm{src[stride*(n-m)]},$

where src is extrapolated with half-sample symmetry.

Definition at line 82 of file gaussian_conv_fir.c.

void fir_free ( fir_coeffs * c )

Release memory associated with fir_coeffs struct.

Parameters

c	fir_coeffs created by fir_precomp()

Definition at line 197 of file gaussian_conv_fir.c.

void fir_gaussian_conv	(	fir_coeffs	c,
		num *	dest,
		const num *	src,
		long	N,
		long	stride
	)

FIR Gaussian convolution.

Parameters

c	fir_coeffs created by fir_precomp()
dest	output convolved data (must be distinct from src)
src	data to be convolved
N	number of samples
stride	stride between successive samples

This routine approximates 1D Gaussian convolution with the FIR filter. The computation itself is performed by conv_sym().

Note: The computation is out-of-place, src and dest must be distinct.

Definition at line 137 of file gaussian_conv_fir.c.

void fir_gaussian_conv_image	(	fir_coeffs	c,
		num *	dest,
		num *	buffer,
		const num *	src,
		int	width,
		int	height,
		int	num_channels
	)

FIR filtering approximation of 2D Gaussian convolution.

Parameters

c	fir_coeffs created by fir_precomp()
dest	destination image
buffer	array with at least width samples
src	source image, must be distinct from dest
width	image width
height	image height
num_channels	number of image channels

Similar to fir_gaussian_conv(), this routine performs 2D FIR-based Gaussian convolution.

Definition at line 158 of file gaussian_conv_fir.c.

int fir_precomp	(	fir_coeffs *	c,
		double	sigma,
		num	tol
	)

Precompute filter coefficients for FIR filtering.

Parameters

c	fir_coeffs pointer to hold precomputed coefficients
sigma	Gaussian standard deviation
tol	filter accuracy (smaller tol implies larger filter)

This routine calls make_g_trunc() to construct the truncated Gaussian FIR filter. The radius of the filter is determined such that

$\lVert g - g^\text{trunc} \rVert_1 \le \mathit{tol}.$

By Young's inequality, the error between convolution using this truncated FIR filter and exact Gaussian convolution is bounded,

$\lVert g * \Tilde{f} - g^\text{trunc} * \Tilde{f} \rVert_\infty \le \mathit{tol} \lVert f \rVert_\infty.$

Definition at line 117 of file gaussian_conv_fir.c.

static num* make_g_trunc	(	num	sigma,
		long	r
	)

static

Construct truncated Gaussian filter for FIR convolution.

Parameters

sigma	Gaussian standard deviation
r	radius of the filter

Returns: pointer to filter, or NULL on failure

This routine constructs a truncated Gaussian 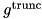$g^\text{trunc}$ for a specified radius r,

$g^\text{trunc}_n = G_\sigma(n) / s(r), \quad s(r) = \sum_{n=-r}^{r} G_\sigma(n).$

The filter should be released by the caller with free().

Definition at line 43 of file gaussian_conv_fir.c.

Detailed Description

Data Structures

Typedefs

Functions

Function Documentation