An accurate recursive filter approximation, computed in-place. More...

Detailed Description

An accurate recursive filter approximation, computed in-place.

This code implements the recursive filter approximation of Gaussian convolution proposed by Vliet, Young, and Verbeek. The Gaussian is approximated by a cascade of a causal filter and an anticausal filter,

$H(z) = G(z) G(z^{-1}), \quad G(z) = \frac{b_0}{1 + a_1 z^{-1} + \cdots + a_K z^{-K}}.$

The process to use these functions is the following:

vyv_precomp() to precompute coefficients for the convolution
vyv_gaussian_conv() or vyv_gaussian_conv_image() to perform the convolution itself (may be called multiple times if desired)

Example: vyv_coeffs c;

vyv_precomp(&c, sigma, K, tol);

vyv_gaussian_conv(c, dest, src, N, stride);

Note: When the num typedef is set to single-precision arithmetic, vyv_gaussian_conv() may be inaccurate for large values of sigma.

References

I.T. Young, L.J. van Vliet, "Recursive implementation of the Gaussian filter," Signal Processing, vol. 44, no. 2, pp. 139-151, 1995. http://dx.doi.org/10.1016/0165-1684(95)00020-E
L.J. van Vliet, I.T. Young, P.W. Verbeek, "Recursive Gaussian derivative filters," Proceedings of the 14th International Conference on Pattern Recognition, vol. 1, pp. 509-514, 1998. http://dx.doi.org/10.1109/ICPR.1998.711192

Data Structures
struct	vyv_coeffs_
	Coefficients for Vliet-Young-Verbeek Gaussian approximation. More...

Macros
#define	VYV_MIN_K 3
	Minimum valid VYV filter order.

#define	VYV_MAX_K 5
	Maximum valid VYV filter order.

#define	VYV_VALID_K(K) (VYV_MIN_K <= (K) && (K) <= VYV_MAX_K)
	Test whether a given K value is a valid VYV filter order.

Typedefs
typedef struct vyv_coeffs_	vyv_coeffs
	Coefficients for Vliet-Young-Verbeek Gaussian approximation. More...

Functions
static double	variance (const complex *poles0, int K, double q)
	Compute the variance of the impulse response. More...

static double	dq_variance (const complex *poles0, int K, double q)
	Derivative of variance with respect to q. More...

static double	compute_q (const complex *poles0, int K, double sigma, double q0)
	Compute q for a desired sigma using Newton's method. More...

static void	expand_pole_product (double c, const complex poles, int K)
	Expand pole product. More...

void	vyv_precomp (vyv_coeffs *c, double sigma, int K, num tol)
	Precomputations for Vliet-Young-Verbeek Gaussian approximation. More...

void	vyv_gaussian_conv (vyv_coeffs c, num dest, const num src, long N, long stride)
	Gaussian convolution Vliet-Young-Verbeek approximation. More...

void	vyv_gaussian_conv_image (vyv_coeffs c, num dest, const num src, int width, int height, int num_channels)
	2D Gaussian convolution Vliet-Young-Verbeek approximation More...

Typedef Documentation

typedef struct vyv_coeffs_ vyv_coeffs

Coefficients for Vliet-Young-Verbeek Gaussian approximation.

The vyv_coeffs struct stores the coefficients for the recursive filter of order K. This struct allows to precompute these filter coefficients separately from actually performing the filtering so that filtering may be performed multiple times using the same precomputed coefficients.

This coefficients struct is precomputed by vyv_precomp() and then used by vyv_gaussian_conv() or vyv_gaussian_conv_image().

Function Documentation

static double compute_q	(	const complex *	poles0,
		int	K,
		double	sigma,
		double	q0
	)

static

Compute q for a desired sigma using Newton's method.

Parameters

poles0	unscaled pole locations
K	number of poles
sigma	the desired sigma
q0	initial estimate of q

Returns: refined value of q

This routine uses Newton's method to solve for the value of q so that the filter achieves the specified variance,

$\operatorname{var}(h) = \sum_{k=1}^K \frac{2 d_k^{1/q}} {(d_k^{1/q} - 1)^2} = \sigma^2,$

where the 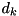$ d_k $ are the unscaled pole locations.

Definition at line 99 of file gaussian_conv_vyv.c.

static double dq_variance	(	const complex *	poles0,
		int	K,
		double	q
	)

static

Derivative of variance with respect to q.

Parameters

poles0	unscaled pole locations
q	rescaling parameter
K	number of poles

Returns: derivative of variance with respect to q

This function is used by compute_q() in solving for q.

Definition at line 66 of file gaussian_conv_vyv.c.

static void expand_pole_product	(	double *	c,
		const complex *	poles,
		int	K
	)

static

Expand pole product.

Parameters

c	resulting filter coefficients
poles	pole locations
K	number of poles

This routine expands the product to obtain the filter coefficients:

$\prod_{k=0}^{K-1}\frac{\mathrm{poles}[k]-1}{\mathrm{poles}[k]-z^{-1}} = \frac{c[0]}{1+\sum_{k=1}^K c[k] z^{-k}}.$

Definition at line 124 of file gaussian_conv_vyv.c.

static double variance	(	const complex *	poles0,
		int	K,
		double	q
	)

static

Compute the variance of the impulse response.

Parameters

poles0	unscaled pole locations
q	rescaling parameter
K	number of poles

Returns: variance achieved by poles = poles0^(1/q)

Definition at line 40 of file gaussian_conv_vyv.c.

void vyv_gaussian_conv	(	vyv_coeffs	c,
		num *	dest,
		const num *	src,
		long	N,
		long	stride
	)

Gaussian convolution Vliet-Young-Verbeek approximation.

Parameters

c	vyv_coeffs created by vyv_precomp()
dest	output convolved data
src	data to be convolved, modified in-place if src = dest
N	number of samples
stride	stride between successive samples

This routine performs Vliet-Young-Verbeek recursive filtering Gaussian convolution approximation. The Gaussian is approximated by a causal filter followed by an anticausal filter,

$H(z) = G(z) G(z^{-1}), \quad G(z) = \frac{b_0}{1 + a_1 z^{-1} + \cdots + a_K z^{-K}}.$

The array c.filter holds the filter coefficients 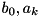$ b_0, a_k $ , which are precomputed by vyv_precomp().

The convolution can be performed in-place by setting src = dest (the source array is overwritten with the result).

Note: When the num typedef is set to single-precision arithmetic, results may be inaccurate for large values of sigma.

Definition at line 259 of file gaussian_conv_vyv.c.

void vyv_gaussian_conv_image	(	vyv_coeffs	c,
		num *	dest,
		const num *	src,
		int	width,
		int	height,
		int	num_channels
	)

2D Gaussian convolution Vliet-Young-Verbeek approximation

Parameters

c	vyv_coeffs created by vyv_precomp()
dest	destination image data
src	source image data, modified in-place if src = dest
width	image width
height	image height
num_channels	number of image channels

Similar to vyv_gaussian_conv(), this routine approximates 2D Gaussian convolution with Vliet-Young-Verbeek recursive filtering.

The convolution can be performed in-place by setting src = dest (the source array is overwritten with the result).

Note: When the num typedef is set to single-precision arithmetic, results may be inaccurate for large values of sigma.

Definition at line 397 of file gaussian_conv_vyv.c.

void vyv_precomp	(	vyv_coeffs *	c,
		double	sigma,
		int	K,
		num	tol
	)

Precomputations for Vliet-Young-Verbeek Gaussian approximation.

Parameters

c	coefficients structure to populate
sigma	the standard deviation of the Gaussian in pixels
K	filter order = 3, 4, or 5
tol	accuracy for initialization on the left boundary

This routine precomputes the filter coefficients for Vliet-Young-Verbeek approximate Gaussian convolution for use in vyv_gaussian_conv() or vyv_gaussian_conv_image(). The filter coefficients are computed by the following steps:

For the specified sigma value, compute_q() solves for the value of q so that the filter achieves the correct variance,
$\operatorname{var}(h) = \sum_{k=1}^K \frac{2 d_k^{1/q}} {(d_k^{1/q} - 1)^2} = \sigma^2,$
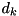where the are the unscaled pole locations.
The pole locations are scaled, $\mathrm{poles}[k] = d_k^{1/q}$ .
The filter is algebraically rearranged by expand_pole_product() as
$\prod_{k=0}^{K-1}\frac{\mathrm{poles}[k]-1}{\mathrm{poles}[k]-z^{-1}} = \frac{c[0]}{1+\sum_{k=1}^K c[k] z^{-k}}.$

For handling the right boundary, the routine precomputes the inverse to the linear system

$u_{N-m} = b_0 q_{N-m} - \sum_{k=1}^K a_k \Tilde{u}_{N-m+k}, \quad m=1,\ldots,K.$

The inverse is stored in matrix c->M, ordered such that

$u_{N-K+m}=\sum_{n=0}^{K-1}M(m,n)\,q_{N-K+m},\quad m=0,\ldots,K-1.$

Definition at line 181 of file gaussian_conv_vyv.c.

Detailed Description

Data Structures

Macros

Typedefs

Functions

Typedef Documentation

Function Documentation